1240. Tiling a Rectangle with the Fewest Squares

Description

Given a rectangle of size n x m, return the minimum number of integer-sided squares that tile the rectangle.

 

Example 1:

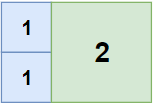
Input: n = 2, m = 3
Output: 3
Explanation: 3 squares are necessary to cover the rectangle.
2 (squares of 1x1)
1 (square of 2x2)

Example 2:

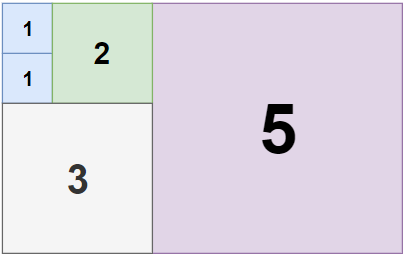
Input: n = 5, m = 8
Output: 5

Example 3:

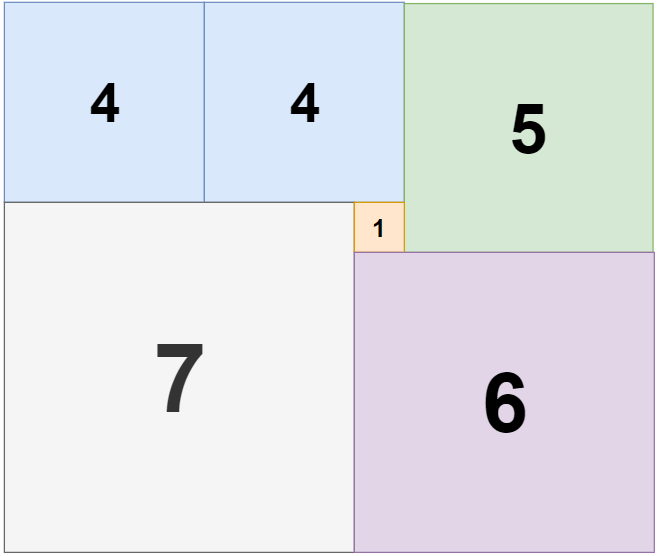
Input: n = 11, m = 13
Output: 6

 

Constraints:

• 1 <= n, m <= 13

 

Solutions

Solution: Backtracking

• Time complexity: O(mn*2^m)
• Space complexity: O(2^m+m)

 

JavaScript

/**
 * @param {number} n
 * @param {number} m
 * @return {number}
 */
const tilingRectangle = function (n, m) {
  const memo = new Map();
  const heights = Array.from({ length: m }, () => 0);

  const getHeightsHash = () => {
    const BASE_HASH = 13;

    return heights.reduce((hash, height) => hash * BASE_HASH + height, 0);
  };

  const tilingRect = () => {
    const hash = getHeightsHash();

    if (memo.has(hash)) return memo.get(hash);
    const minHeight = Math.min(...heights);

    if (minHeight === n) return 0;
    const start = heights.indexOf(minHeight);
    let result = m * n;

    for (let length = 1; length <= Math.min(m - start, n - minHeight); length++) {
      if (heights.slice(start, start + length).some(height => height !== minHeight)) break;

      for (let index = start; index < start + length; index++) {
        heights[index] += length;
      }
      result = Math.min(tilingRect(), result);

      for (let index = start; index < start + length; index++) {
        heights[index] -= length;
      }
    }
    memo.set(hash, result + 1);
    return result + 1;
  };

  return tilingRect();
};