834. Sum of Distances in Tree

Description

There is an undirected connected tree with n nodes labeled from 0 to n - 1 and n - 1 edges.

You are given the integer n and the array edges where edges[i] = [ai, bi] indicates that there is an edge between nodes ai and bi in the tree.

Return an array answer of length n where answer[i] is the sum of the distances between the ith node in the tree and all other nodes.

 

Example 1:

Input: n = 6, edges = [[0,1],[0,2],[2,3],[2,4],[2,5]]
Output: [8,12,6,10,10,10]
Explanation: The tree is shown above.
We can see that dist(0,1) + dist(0,2) + dist(0,3) + dist(0,4) + dist(0,5)
equals 1 + 1 + 2 + 2 + 2 = 8.
Hence, answer[0] = 8, and so on.

Example 2:

Input: n = 1, edges = []
Output: [0]

Example 3:

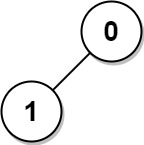
Input: n = 2, edges = [[1,0]]
Output: [1,1]

 

Constraints:

• 1 <= n <= 3 * 104
• edges.length == n - 1
• edges[i].length == 2
• 0 <= ai, bi < n
• ai != bi
• The given input represents a valid tree.

 

Solutions

Solution: Depth-First Search + Dynamic Programming

• Time complexity: O(n)
• Space complexity: O(n)

 

JavaScript

/**
 * @param {number} n
 * @param {number[][]} edges
 * @return {number[]}
 */
const sumOfDistancesInTree = function (n, edges) {
  const graph = new Array(n)
    .fill('')
    .map(_ => []);

  for (const [a, b] of edges) {
    graph[a].push(b);
    graph[b].push(a);
  }
  const counts = new Array(n).fill(1);
  const result = new Array(n).fill(0);
  const root = 0;

  const dfsGraph = (node, parent) => {
    for (const connectedNode of graph[node]) {
      if (connectedNode === parent) continue;
      dfsGraph(connectedNode, node);
      counts[node] += counts[connectedNode];
      result[node] += result[connectedNode] + counts[connectedNode];
    }
  };

  dfsGraph(root, null);

  const sumDistance = (node, parent) => {
    for (const connectedNode of graph[node]) {
      if (connectedNode === parent) continue;
      result[connectedNode] = result[node] - counts[connectedNode] + n - counts[connectedNode];
      sumDistance(connectedNode, node);
    }
  };

  sumDistance(root, null);
  return result;
};