587. Erect the Fence

Description

You are given an array trees where trees[i] = [xi, yi] represents the location of a tree in the garden.

Fence the entire garden using the minimum length of rope, as it is expensive. The garden is well-fenced only if all the trees are enclosed.

Return the coordinates of trees that are exactly located on the fence perimeter. You may return the answer in any order.

 

Example 1:

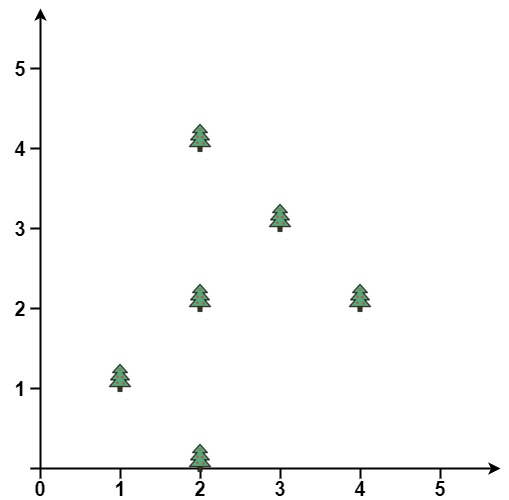
Input: trees = [[1,1],[2,2],[2,0],[2,4],[3,3],[4,2]]
Output: [[1,1],[2,0],[4,2],[3,3],[2,4]]
Explanation: All the trees will be on the perimeter of the fence except the tree at [2, 2], which will be inside the fence.

Example 2:

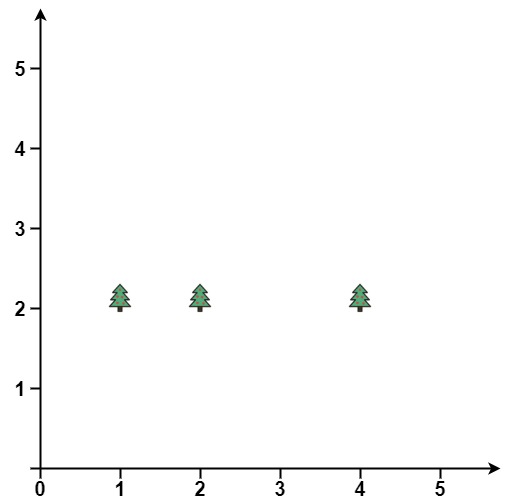
Input: trees = [[1,2],[2,2],[4,2]]
Output: [[4,2],[2,2],[1,2]]
Explanation: The fence forms a line that passes through all the trees.

 

Constraints:

• 1 <= trees.length <= 3000
• trees[i].length == 2
• 0 <= xi, yi <= 100
• All the given positions are unique.

 

Solutions

Solution: Monotone Chain Algorithm

• Time complexity: O(nlogn)
• Space complexity: O(n)

 

JavaScript

/**
 * @param {number[][]} trees
 * @return {number[][]}
 */
const outerTrees = function (trees) {
  const n = trees.length;

  if (n <= 1) return trees;

  const crossProduct = (a, b, c) => {
    const BAx = a[0] - b[0];
    const BAy = a[1] - b[1];
    const BCx = c[0] - b[0];
    const BCy = c[1] - b[1];

    return BAx * BCy - BAy * BCx;
  };

  trees.sort((a, b) => a[0] - b[0] || a[1] - b[1]);

  const lower = [];
  const upper = [];

  for (const point of trees) {
    while (lower.length >= 2 && crossProduct(lower.at(-2), lower.at(-1), point) < 0) {
      lower.pop();
    }
    lower.push(point);
  }

  for (let index = n - 1; index >= 0; index--) {
    const point = trees[index];

    while (upper.length >= 2 && crossProduct(upper.at(-2), upper.at(-1), point) < 0) {
      upper.pop();
    }
    upper.push(point);
  }

  return [...new Set([...lower, ...upper])];
};