1382. Balance a Binary Search Tree

Description

Given the root of a binary search tree, return a balanced binary search tree with the same node values. If there is more than one answer, return any of them.

A binary search tree is balanced if the depth of the two subtrees of every node never differs by more than 1.

 

Example 1:

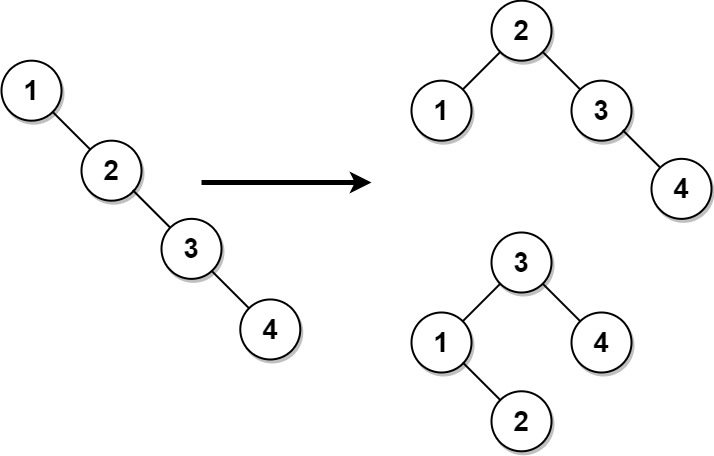
Input: root = [1,null,2,null,3,null,4,null,null]
Output: [2,1,3,null,null,null,4]
Explanation: This is not the only correct answer, [3,1,4,null,2] is also correct.

Example 2:

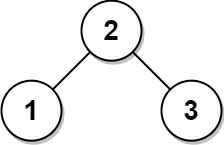
Input: root = [2,1,3]
Output: [2,1,3]

 

Constraints:

• The number of nodes in the tree is in the range [1, 104].
• 1 <= Node.val <= 105

 

Solutions

Solution: Depth-First Search

• Time complexity: O(n)
• Space complexity: O(n)

 

JavaScript

/**
 * Definition for a binary tree node.
 * function TreeNode(val, left, right) {
 *     this.val = (val===undefined ? 0 : val)
 *     this.left = (left===undefined ? null : left)
 *     this.right = (right===undefined ? null : right)
 * }
 */
/**
 * @param {TreeNode} root
 * @return {TreeNode}
 */
const balanceBST = function (root) {
  const values = [];
  const getBSTValue = node => {
    if (!node) return;
    const { val, left, right } = node;

    values.push(val);
    getBSTValue(left);
    getBSTValue(right);
  };

  getBSTValue(root);
  values.sort((a, b) => a - b);

  const createBST = (start, end) => {
    if (start > end) return null;
    const mid = Math.floor((start + end) / 2);
    const node = new TreeNode(values[mid]);

    node.left = createBST(start, mid - 1);
    node.right = createBST(mid + 1, end);
    return node;
  };

  return createBST(0, values.length - 1);
};