840. Magic Squares In Grid

Description

A 3 x 3 magic square is a 3 x 3 grid filled with distinct numbers from 1 to 9 such that each row, column, and both diagonals all have the same sum.

Given a row x col grid of integers, how many 3 x 3 contiguous magic square subgrids are there?

Note: while a magic square can only contain numbers from 1 to 9, grid may contain numbers up to 15.

 

Example 1:

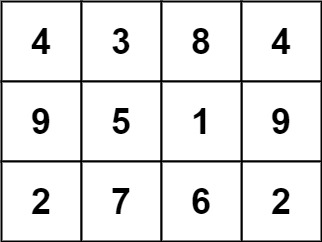
Input: grid = [[4,3,8,4],[9,5,1,9],[2,7,6,2]]
Output: 1
Explanation: 
The following subgrid is a 3 x 3 magic square:

while this one is not:

In total, there is only one magic square inside the given grid.

Example 2:

Input: grid = [[8]]
Output: 0

 

Constraints:

• row == grid.length
• col == grid[i].length
• 1 <= row, col <= 10
• 0 <= grid[i][j] <= 15

 

Solutions

Solution: Math

• Time complexity: O(mn)
• Space complexity: O(1)

 

JavaScript

/**
 * @param {number[][]} grid
 * @return {number}
 */
const numMagicSquaresInside = function (grid) {
  const m = grid.length;
  const n = grid[0].length;
  let result = 0;

  const isMagicSquare = (centerRow, centerCol) => {
    if (grid[centerRow][centerCol] !== 5) return false;

    const numSet = new Set();

    for (let a = -1; a <= 1; a++) {
      let sum1 = 0;
      let sum2 = 0;

      for (let b = -1; b <= 1; b++) {
        const num1 = grid[centerRow + a][centerCol + b];
        const num2 = grid[centerRow + b][centerCol + a];

        if (num1 < 1 || num1 > 9 || num2 < 1 || num2 > 9 || numSet.has(num1)) return false;

        sum1 += num1;
        sum2 += num2;
        numSet.add(num1);
      }

      if (sum1 !== 15 || sum2 !== 15) return false;
    }

    let diagonalSum1 = 0;
    let diagonalSum2 = 0;

    for (let index = -1; index <= 1; index++) {
      diagonalSum1 += grid[centerRow + index][centerCol + index];
      diagonalSum2 += grid[centerRow + index][centerCol - index];
    }

    return diagonalSum1 === 15 && diagonalSum2 === 15;
  };

  for (let row = 1; row < m - 1; row++) {
    for (let col = 1; col < n - 1; col++) {
      if (isMagicSquare(row, col)) {
        result += 1;
      }
    }
  }

  return result;
};