1192. Critical Connections in a Network
Description
There are n servers numbered from 0 to n - 1 connected by undirected server-to-server connections forming a network where connections[i] = [ai, bi] represents a connection between servers ai and bi. Any server can reach other servers directly or indirectly through the network.
A critical connection is a connection that, if removed, will make some servers unable to reach some other server.
Return all critical connections in the network in any order.
Example 1:
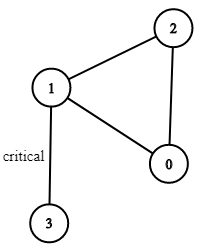
Input: n = 4, connections = [[0,1],[1,2],[2,0],[1,3]] Output: [[1,3]] Explanation: [[3,1]] is also accepted.
Example 2:
Input: n = 2, connections = [[0,1]] Output: [[0,1]]
Constraints:
2 <= n <= 105n - 1 <= connections.length <= 1050 <= ai, bi <= n - 1ai != bi- There are no repeated connections.
Solutions
Solution: Biconnected Component
- Time complexity: O(n + connections.length)
- Space complexity: O(n + connections.length)
JavaScript
js
/**
* @param {number} n
* @param {number[][]} connections
* @return {number[][]}
*/
const criticalConnections = function (n, connections) {
const network = Array.from({ length: n }, () => []);
for (const [a, b] of connections) {
network[a].push(b);
network[b].push(a);
}
const times = Array.from({ length: n }, () => 0);
const low = Array.from({ length: n }, () => 0);
const result = [];
let time = 1;
const biconnectedComponent = (node, parent) => {
times[node] = time;
low[node] = time;
time += 1;
for (const next of network[node]) {
if (!times[next]) {
biconnectedComponent(next, node);
low[node] = Math.min(low[node], low[next]);
} else if (next !== parent) {
low[node] = Math.min(low[node], times[next]);
}
if (low[next] > times[node]) {
result.push([node, next]);
}
}
};
biconnectedComponent(0, -1);
return result;
};