1627. Graph Connectivity With Threshold

Description

We have n cities labeled from 1 to n. Two different cities with labels x and y are directly connected by a bidirectional road if and only if x and y share a common divisor strictly greater than some threshold. More formally, cities with labels x and y have a road between them if there exists an integer z such that all of the following are true:

• x % z == 0,
• y % z == 0, and
• z > threshold.

Given the two integers, n and threshold, and an array of queries, you must determine for each queries[i] = [ai, bi] if cities ai and bi are connected directly or indirectly. (i.e. there is some path between them).

Return an array answer, where answer.length == queries.length and answer[i] is true if for the ith query, there is a path between ai and bi, or answer[i] is false if there is no path.

 

Example 1:

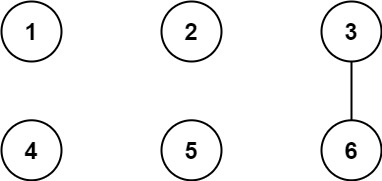
Input: n = 6, threshold = 2, queries = [[1,4],[2,5],[3,6]]
Output: [false,false,true]
Explanation: The divisors for each number:
1:   1
2:   1, 2
3:   1, 3
4:   1, 2, 4
5:   1, 5
6:   1, 2, 3, 6
Using the underlined divisors above the threshold, only cities 3 and 6 share a common divisor, so they are the
only ones directly connected. The result of each query:
[1,4]   1 is not connected to 4
[2,5]   2 is not connected to 5
[3,6]   3 is connected to 6 through path 3--6

Example 2:

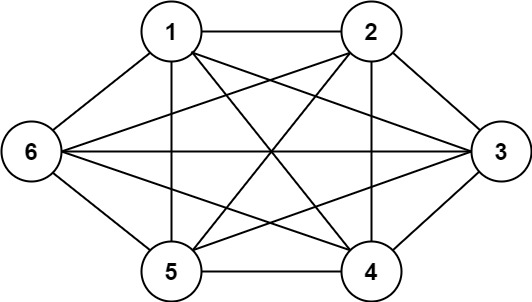
Input: n = 6, threshold = 0, queries = [[4,5],[3,4],[3,2],[2,6],[1,3]]
Output: [true,true,true,true,true]
Explanation: The divisors for each number are the same as the previous example. However, since the threshold is 0,
all divisors can be used. Since all numbers share 1 as a divisor, all cities are connected.

Example 3:

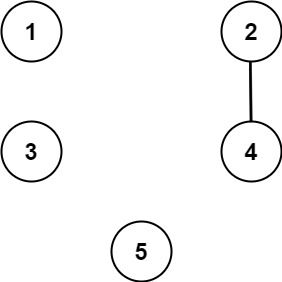
Input: n = 5, threshold = 1, queries = [[4,5],[4,5],[3,2],[2,3],[3,4]]
Output: [false,false,false,false,false]
Explanation: Only cities 2 and 4 share a common divisor 2 which is strictly greater than the threshold 1, so they are the only ones directly connected.
Please notice that there can be multiple queries for the same pair of nodes [x, y], and that the query [x, y] is equivalent to the query [y, x].

 

Constraints:

• 2 <= n <= 104
• 0 <= threshold <= n
• 1 <= queries.length <= 105
• queries[i].length == 2
• 1 <= ai, bi <= cities
• ai != bi

 

Solutions

Solution: Union Find

• Time complexity: O(nlogn+queries.length)
• Space complexity: O(n)

 

JavaScript

/**
 * @param {number} n
 * @param {number} threshold
 * @param {number[][]} queries
 * @return {boolean[]}
 */
const areConnected = function (n, threshold, queries) {
  const graph = new UnionFind(n + 1);

  for (let factor = threshold + 1; factor <= n; factor++) {
    for (let value = factor * 2; value <= n; value += factor) {
      graph.union(factor, value);
    }
  }

  return queries.map(([a, b]) => graph.find(a) === graph.find(b));
};

class UnionFind {
  constructor(n) {
    this.groups = Array.from({ length: n }, (_, index) => index);
    this.ranks = Array.from({ length: n }, () => 0);
  }

  find(node) {
    if (this.groups[node] === node) return node;

    this.groups[node] = this.find(this.groups[node]);

    return this.groups[node];
  }

  union(a, b) {
    const groupA = this.find(a);
    const groupB = this.find(b);

    if (groupA === groupB) return false;
    if (this.ranks[groupA] > this.ranks[groupB]) {
      this.groups[groupB] = groupA;
    } else if (this.ranks[groupB] > this.ranks[groupA]) {
      this.groups[groupA] = groupB;
    } else {
      this.groups[groupB] = groupA;
      this.ranks[groupA] += 1;
    }

    return true;
  }
}