2360. Longest Cycle in a Graph

Description

You are given a directed graph of n nodes numbered from 0 to n - 1, where each node has at most one outgoing edge.

The graph is represented with a given 0-indexed array edges of size n, indicating that there is a directed edge from node i to node edges[i]. If there is no outgoing edge from node i, then edges[i] == -1.

Return the length of the longest cycle in the graph. If no cycle exists, return -1.

A cycle is a path that starts and ends at the same node.

 

Example 1:

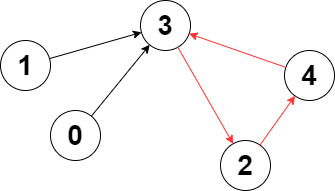
Input: edges = [3,3,4,2,3]
Output: 3
Explanation: The longest cycle in the graph is the cycle: 2 -> 4 -> 3 -> 2.
The length of this cycle is 3, so 3 is returned.

Example 2:

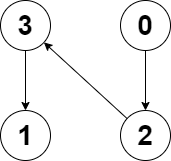
Input: edges = [2,-1,3,1]
Output: -1
Explanation: There are no cycles in this graph.

 

Constraints:

• n == edges.length
• 2 <= n <= 105
• -1 <= edges[i] < n
• edges[i] != i

 

Solutions

Solution: Depth-First Search

• Time complexity: O(n)
• Space complexity: O(n)

 

JavaScript

/**
 * @param {number[]} edges
 * @return {number}
 */
const longestCycle = function (edges) {
  const n = edges.length;
  const visitedTime = Array.from({ length: n }, () => 0);
  let time = 1;
  let result = -1;

  for (let index = 0; index < n; index++) {
    if (visitedTime[index]) continue;

    const startTime = time;
    let node = index;

    while (node !== -1 && !visitedTime[node]) {
      visitedTime[node] = time;
      node = edges[node];
      time += 1;
    }

    if (node !== -1 && visitedTime[node] >= startTime) {
      const len = time - visitedTime[node];

      result = Math.max(len, result);
    }
  }

  return result;
};