3459. Length of Longest V-Shaped Diagonal Segment

Description

You are given a 2D integer matrix grid of size n x m, where each element is either 0, 1, or 2.

A V-shaped diagonal segment is defined as:

• The segment starts with 1.
• The subsequent elements follow this infinite sequence: 2, 0, 2, 0, ....
• The segment:
  • Starts along a diagonal direction (top-left to bottom-right, bottom-right to top-left, top-right to bottom-left, or bottom-left to top-right).
  • Continues the sequence in the same diagonal direction.
  • Makes at most one clockwise 90-degree turn to another diagonal direction while maintaining the sequence.

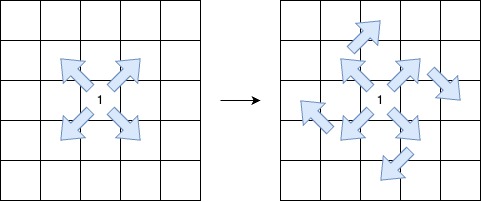
Return the length of the longest V-shaped diagonal segment. If no valid segment exists, return 0.

 

Example 1:

Input: grid = [[2,2,1,2,2],[2,0,2,2,0],[2,0,1,1,0],[1,0,2,2,2],[2,0,0,2,2]]

Output: 5

Explanation:

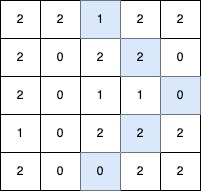
The longest V-shaped diagonal segment has a length of 5 and follows these coordinates: (0,2) → (1,3) → (2,4), takes a 90-degree clockwise turn at (2,4), and continues as (3,3) → (4,2).

Example 2:

Input: grid = [[2,2,2,2,2],[2,0,2,2,0],[2,0,1,1,0],[1,0,2,2,2],[2,0,0,2,2]]

Output: 4

Explanation:

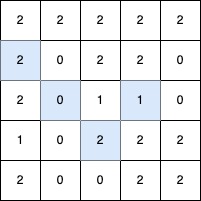
The longest V-shaped diagonal segment has a length of 4 and follows these coordinates: (2,3) → (3,2), takes a 90-degree clockwise turn at (3,2), and continues as (2,1) → (1,0).

Example 3:

Input: grid = [[1,2,2,2,2],[2,2,2,2,0],[2,0,0,0,0],[0,0,2,2,2],[2,0,0,2,0]]

Output: 5

Explanation:

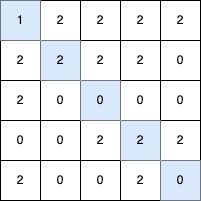
The longest V-shaped diagonal segment has a length of 5 and follows these coordinates: (0,0) → (1,1) → (2,2) → (3,3) → (4,4).

Example 4:

Input: grid = [[1]]

Output: 1

Explanation:

The longest V-shaped diagonal segment has a length of 1 and follows these coordinates: (0,0).

 

Constraints:

• n == grid.length
• m == grid[i].length
• 1 <= n, m <= 500
• grid[i][j] is either 0, 1 or 2.

 

Solutions

Solution: Dynamic Programming

• Time complexity: O(8mn -> mn)
• Space complexity: O(8mn -> mn)

 

JavaScript

/**
 * @param {number[][]} grid
 * @return {number}
 */
const lenOfVDiagonal = function (grid) {
  const m = grid.length;
  const n = grid[0].length;
  const directions = [
    [1, 1],
    [1, -1],
    [-1, -1],
    [-1, 1],
  ];
  const dp = new Array(m * n * 4 * 2).fill(-1);
  let result = 0;

  const getVDiagonalSegment = (row, col, dir, turned, target) => {
    if (row < 0 || col < 0 || row >= m || col >= n) return 0;
    if (grid[row][col] !== target) return 0;

    const hashKey = ((row * n + col) * 4 + dir) * 2 + turned;

    if (dp[hashKey] !== -1) return dp[hashKey];

    const [moveRow, moveCol] = directions[dir];
    const nextRow = row + moveRow;
    const nextCol = col + moveCol;
    const nextValue = target ? 0 : 2;
    let maxSegment = 1 + getVDiagonalSegment(nextRow, nextCol, dir, turned, nextValue);

    if (!turned) {
      const turnDir = (dir + 1) % 4;
      const [moveRow, moveCol] = directions[turnDir];
      const turnRow = row + moveRow;
      const turnCol = col + moveCol;
      const len = 1 + getVDiagonalSegment(turnRow, turnCol, turnDir, 1, nextValue);

      maxSegment = Math.max(len, maxSegment);
    }

    dp[hashKey] = maxSegment;

    return maxSegment;
  };

  for (let row = 0; row < m; row++) {
    for (let col = 0; col < n; col++) {
      if (grid[row][col] !== 1) continue;

      for (let index = 0; index < 4; index++) {
        const [moveRow, moveCol] = directions[index];
        const nextRow = row + moveRow;
        const nextCol = col + moveCol;
        const len = 1 + getVDiagonalSegment(nextRow, nextCol, index, 0, 2);

        result = Math.max(len, result);
      }
    }
  }

  return result;
};