2054. Two Best Non-Overlapping Events

Description

You are given a 0-indexed 2D integer array of events where events[i] = [startTimei, endTimei, valuei]. The ith event starts at startTimeiand ends at endTimei, and if you attend this event, you will receive a value of valuei. You can choose at most two non-overlapping events to attend such that the sum of their values is maximized.

Return this maximum sum.

Note that the start time and end time is inclusive: that is, you cannot attend two events where one of them starts and the other ends at the same time. More specifically, if you attend an event with end time t, the next event must start at or after t + 1.

 

Example 1:

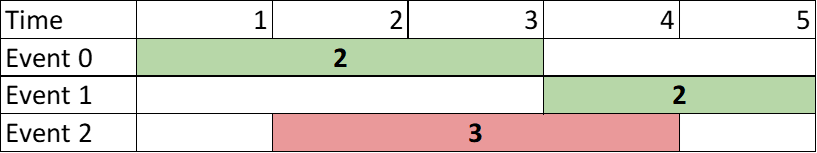
Input: events = [[1,3,2],[4,5,2],[2,4,3]]
Output: 4
Explanation: Choose the green events, 0 and 1 for a sum of 2 + 2 = 4.

Example 2:

Input: events = [[1,3,2],[4,5,2],[1,5,5]]
Output: 5
Explanation: Choose event 2 for a sum of 5.

Example 3:

Input: events = [[1,5,3],[1,5,1],[6,6,5]]
Output: 8
Explanation: Choose events 0 and 2 for a sum of 3 + 5 = 8.

 

Constraints:

• 2 <= events.length <= 105
• events[i].length == 3
• 1 <= startTimei <= endTimei <= 109
• 1 <= valuei <= 106

 

Solutions

Solution: Sorting

• Time complexity: O(nlogn)
• Space complexity: O(n)

 

JavaScript

/**
 * @param {number[][]} events
 * @return {number}
 */
const maxTwoEvents = function (events) {
  const endEventMap = events.reduce((map, [_, end, value]) => {
    const previousValue = map.get(end);

    if (previousValue >= value) return map;
    return map.set(end, value);
  }, new Map());
  const endEvents = [...endEventMap.keys()];
  let previousValue = 0;
  let result = 0;
  let currentEnd = 0;

  events.sort((a, b) => a[0] - b[0]);
  endEvents.sort((a, b) => a - b);

  for (const [start, end, value] of events) {

    while (endEvents[currentEnd] < start) {
      const endValue = endEventMap.get(endEvents[currentEnd]);

      previousValue = Math.max(endValue, previousValue);
      currentEnd += 1;
    }
    result = Math.max(previousValue + value, result);
  }
  return result;
};