1631. Path With Minimum Effort

Description

You are a hiker preparing for an upcoming hike. You are given heights, a 2D array of size rows x columns, where heights[row][col] represents the height of cell (row, col). You are situated in the top-left cell, (0, 0), and you hope to travel to the bottom-right cell, (rows-1, columns-1) (i.e., 0-indexed). You can move up, down, left, or right, and you wish to find a route that requires the minimum effort.

A route's effort is the maximum absolute differencein heights between two consecutive cells of the route.

Return the minimum effort required to travel from the top-left cell to the bottom-right cell.

 

Example 1:

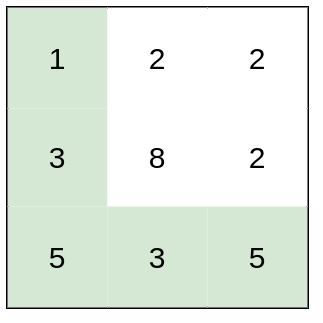
Input: heights = [[1,2,2],[3,8,2],[5,3,5]]
Output: 2
Explanation: The route of [1,3,5,3,5] has a maximum absolute difference of 2 in consecutive cells.
This is better than the route of [1,2,2,2,5], where the maximum absolute difference is 3.

Example 2:

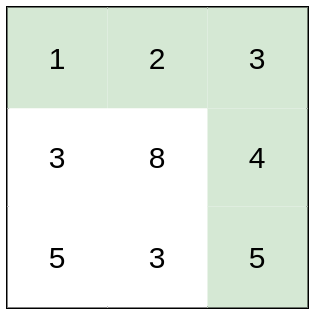
Input: heights = [[1,2,3],[3,8,4],[5,3,5]]
Output: 1
Explanation: The route of [1,2,3,4,5] has a maximum absolute difference of 1 in consecutive cells, which is better than route [1,3,5,3,5].

Example 3:

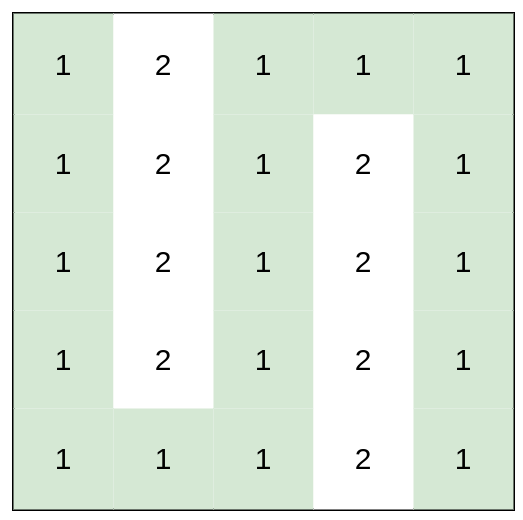
Input: heights = [[1,2,1,1,1],[1,2,1,2,1],[1,2,1,2,1],[1,2,1,2,1],[1,1,1,2,1]]
Output: 0
Explanation: This route does not require any effort.

 

Constraints:

• rows == heights.length
• columns == heights[i].length
• 1 <= rows, columns <= 100
• 1 <= heights[i][j] <= 106

 

Solutions

Solution: Depth-First Search + Binary Search

• Time complexity: O(m∗nlogheight)
• Space complexity: O(m∗n)

 

JavaScript

/**
 * @param {number[][]} heights
 * @return {number}
 */
const minimumEffortPath = function (heights) {
  const m = heights.length;
  const n = heights[0].length;
  const visited = new Set();
  const isMiniEffort = (row, col, limit, preHeight) => {
    if (row >= m || col >= n || (row < 0) | (col < 0)) return false;
    const position = `${row}_${col}`;
    const height = heights[row][col];

    if (visited.has(position)) return false;
    if (Math.abs(height - preHeight) > limit) return false;
    if (row === m - 1 && col === n - 1) return true;
    visited.add(position);
    return (
      isMiniEffort(row - 1, col, limit, height) ||
      isMiniEffort(row + 1, col, limit, height) ||
      isMiniEffort(row, col - 1, limit, height) ||
      isMiniEffort(row, col + 1, limit, height)
    );
  };
  let left = 0;
  let right = 10 ** 6;

  while (left < right) {
    const mid = Math.floor((left + right) / 2);

    visited.clear();
    isMiniEffort(0, 0, mid, heights[0][0]) ? (right = mid) : (left = mid + 1);
  }
  return left;
};