1368. Minimum Cost to Make at Least One Valid Path in a Grid

Description

Given an m x n grid. Each cell of the grid has a sign pointing to the next cell you should visit if you are currently in this cell. The sign of grid[i][j] can be:

• 1 which means go to the cell to the right. (i.e go from grid[i][j] to grid[i][j + 1])
• 2 which means go to the cell to the left. (i.e go from grid[i][j] to grid[i][j - 1])
• 3 which means go to the lower cell. (i.e go from grid[i][j] to grid[i + 1][j])
• 4 which means go to the upper cell. (i.e go from grid[i][j] to grid[i - 1][j])

Notice that there could be some signs on the cells of the grid that point outside the grid.

You will initially start at the upper left cell (0, 0). A valid path in the grid is a path that starts from the upper left cell (0, 0) and ends at the bottom-right cell (m - 1, n - 1) following the signs on the grid. The valid path does not have to be the shortest.

You can modify the sign on a cell with cost = 1. You can modify the sign on a cell one time only.

Return the minimum cost to make the grid have at least one valid path.

 

Example 1:

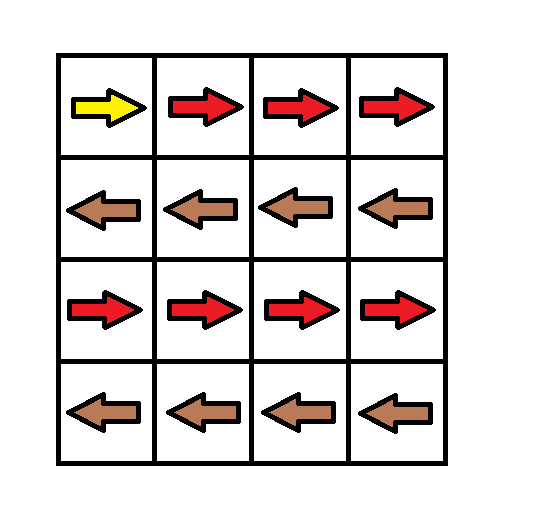
Input: grid = [[1,1,1,1],[2,2,2,2],[1,1,1,1],[2,2,2,2]]
Output: 3
Explanation: You will start at point (0, 0).
The path to (3, 3) is as follows. (0, 0) --> (0, 1) --> (0, 2) --> (0, 3) change the arrow to down with cost = 1 --> (1, 3) --> (1, 2) --> (1, 1) --> (1, 0) change the arrow to down with cost = 1 --> (2, 0) --> (2, 1) --> (2, 2) --> (2, 3) change the arrow to down with cost = 1 --> (3, 3)
The total cost = 3.

Example 2:

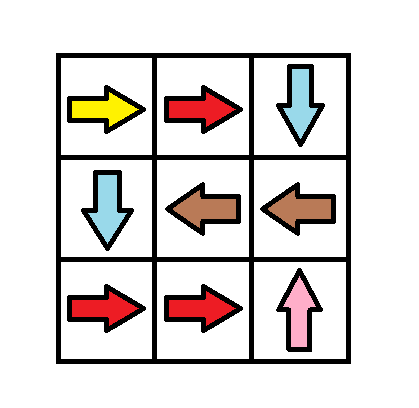
Input: grid = [[1,1,3],[3,2,2],[1,1,4]]
Output: 0
Explanation: You can follow the path from (0, 0) to (2, 2).

Example 3:

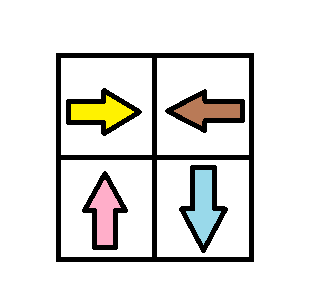
Input: grid = [[1,2],[4,3]]
Output: 1

 

Constraints:

• m == grid.length
• n == grid[i].length
• 1 <= m, n <= 100
• 1 <= grid[i][j] <= 4

 

Solutions

Solution: Breadth-First Search + Priority Queue

• Time complexity: O(mn*log(mn))
• Space complexity: O(mn)

 

JavaScript

/**
 * @param {number[][]} grid
 * @return {number}
 */
const minCost = function (grid) {
  const RIGHT = 1;
  const LEFT = 2;
  const LOWER = 3;
  const UPPER = 4;

  const m = grid.length;
  const n = grid[0].length;
  const directions = [
    [0, 1, LOWER],
    [1, 0, RIGHT],
    [0, -1, UPPER],
    [-1, 0, LEFT],
  ];
  const queue = new MinPriorityQueue({ priority: ({ cost }) => cost });
  const costs = Array.from({ length: m }, () => new Array(n).fill(Number.MAX_SAFE_INTEGER));

  queue.enqueue({ row: 0, col: 0, cost: 0 });
  costs[0][0] = 0;

  while (queue.size()) {
    const { row, col, cost } = queue.dequeue().element;
    const cell = grid[row][col];

    if (row === m - 1 && col === n - 1) return cost;

    for (const [moveCol, moveRow, sign] of directions) {
      const nextCol = col + moveCol;
      const nextRow = row + moveRow;

      if (nextCol >= n || nextRow >= m || nextCol < 0 || nextRow < 0) continue;
      const isChangeSign = cell !== sign;
      const nextCost = isChangeSign ? cost + 1 : cost;

      if (costs[nextRow][nextCol] <= nextCost) continue;

      queue.enqueue({ row: nextRow, col: nextCol, cost: nextCost });
      costs[nextRow][nextCol] = nextCost;
    }
  }
  return -1;
};