1766. Tree of Coprimes

Description

There is a tree (i.e., a connected, undirected graph that has no cycles) consisting of n nodes numbered from 0 to n - 1 and exactly n - 1 edges. Each node has a value associated with it, and the root of the tree is node 0.

To represent this tree, you are given an integer array nums and a 2D array edges. Each nums[i] represents the ith node's value, and each edges[j] = [uj, vj] represents an edge between nodes uj and vj in the tree.

Two values x and y are coprime if gcd(x, y) == 1 where gcd(x, y) is the greatest common divisor of x and y.

An ancestor of a node i is any other node on the shortest path from node i to the root. A node is not considered an ancestor of itself.

Return an array ans of size n, where ans[i] is the closest ancestor to node i such that nums[i] and nums[ans[i]] are coprime, or -1 if there is no such ancestor.

 

Example 1:

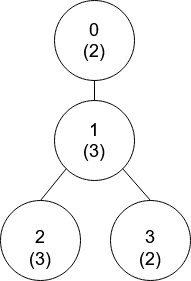
Input: nums = [2,3,3,2], edges = [[0,1],[1,2],[1,3]]
Output: [-1,0,0,1]
Explanation: In the above figure, each node's value is in parentheses.
- Node 0 has no coprime ancestors.
- Node 1 has only one ancestor, node 0. Their values are coprime (gcd(2,3) == 1).
- Node 2 has two ancestors, nodes 1 and 0. Node 1's value is not coprime (gcd(3,3) == 3), but node 0's
  value is (gcd(2,3) == 1), so node 0 is the closest valid ancestor.
- Node 3 has two ancestors, nodes 1 and 0. It is coprime with node 1 (gcd(3,2) == 1), so node 1 is its
  closest valid ancestor.

Example 2:

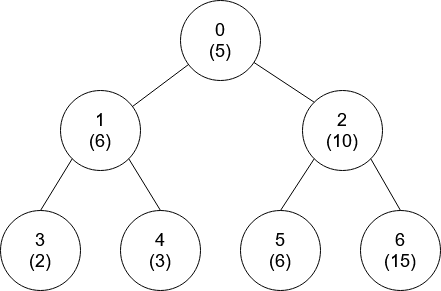
Input: nums = [5,6,10,2,3,6,15], edges = [[0,1],[0,2],[1,3],[1,4],[2,5],[2,6]]
Output: [-1,0,-1,0,0,0,-1]

 

Constraints:

• nums.length == n
• 1 <= nums[i] <= 50
• 1 <= n <= 105
• edges.length == n - 1
• edges[j].length == 2
• 0 <= uj, vj < n
• uj != vj

 

Solutions

Solution: Depth-First Search

• Time complexity: O(n*Max(nums))
• Space complexity: O(n+Max(nums))

 

JavaScript

/**
 * @param {number[]} nums
 * @param {number[][]} edges
 * @return {number[]}
 */
const getCoprimes = function (nums, edges) {
  const n = nums.length;
  const tree = Array.from({ length: n }, () => []);
  const maxNum = Math.max(...nums);
  const stack = Array.from({ length: maxNum + 1 }, () => []);
  const result = Array.from({ length: n }, () => -1);

  for (const [u, v] of edges) {
    tree[u].push(v);
    tree[v].push(u);
  }

  const gcd = (a, b) => (b ? gcd(b, a % b) : a);

  const getAncestor = node => {
    let maxDepth = -1;
    let result = -1;

    for (let num = 1; num <= maxNum; num++) {
      if (!stack[num].length) continue;
      const ancestor = stack[num].at(-1);

      if (ancestor.depth > maxDepth && gcd(nums[node], num) === 1) {
        maxDepth = ancestor.depth;
        result = ancestor.node;
      }
    }

    return result;
  };

  const dfsTree = (node, prev, depth) => {
    const num = nums[node];

    result[node] = getAncestor(node);
    stack[num].push({ node, depth });

    for (const neighbor of tree[node]) {
      if (neighbor === prev) continue;

      dfsTree(neighbor, node, depth + 1);
    }

    stack[num].pop();
  };

  dfsTree(0, -1, 0);

  return result;
};