1326. Minimum Number of Taps to Open to Water a Garden

Description

There is a one-dimensional garden on the x-axis. The garden starts at the point 0 and ends at the point n. (i.e., the length of the garden is n).

There are n + 1 taps located at points [0, 1, ..., n] in the garden.

Given an integer n and an integer array ranges of length n + 1 where ranges[i] (0-indexed) means the i-th tap can water the area [i - ranges[i], i + ranges[i]] if it was open.

Return the minimum number of taps that should be open to water the whole garden, If the garden cannot be watered return -1.

 

Example 1:

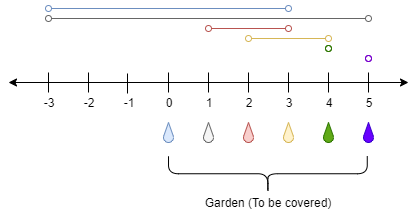
Input: n = 5, ranges = [3,4,1,1,0,0]
Output: 1
Explanation: The tap at point 0 can cover the interval [-3,3]
The tap at point 1 can cover the interval [-3,5]
The tap at point 2 can cover the interval [1,3]
The tap at point 3 can cover the interval [2,4]
The tap at point 4 can cover the interval [4,4]
The tap at point 5 can cover the interval [5,5]
Opening Only the second tap will water the whole garden [0,5]

Example 2:

Input: n = 3, ranges = [0,0,0,0]
Output: -1
Explanation: Even if you activate all the four taps you cannot water the whole garden.

 

Constraints:

• 1 <= n <= 104
• ranges.length == n + 1
• 0 <= ranges[i] <= 100

 

Solutions

Solution: Greedy

• Time complexity: O(n)
• Space complexity: O(n)

 

JavaScript

/**
 * @param {number} n
 * @param {number[]} ranges
 * @return {number}
 */
const minTaps = function (n, ranges) {
  const intervals = Array.from({ length: n + 1 }, () => 0);

  for (let index = 0; index <= n; index++) {
    const range = ranges[index];
    const start = Math.max(index - range, 0);
    const end = Math.min(index + range, n);

    intervals[start] = Math.max(end - start, intervals[start]);
  }
  let end = 0;
  let farthest = 0;
  let result = 0;

  for (let index = 0; index < n; index++) {
    farthest = Math.max(index + intervals[index], farthest);

    if (index === end) {
      end = farthest;
      result += 1;
    }
  }
  return end === n ? result : -1;
};