1975. Maximum Matrix Sum

Description

You are given an n x n integer matrix. You can do the following operation any number of times:

• Choose any two adjacent elements of matrix and multiply each of them by -1.

Two elements are considered adjacent if and only if they share a border.

Your goal is to maximize the summation of the matrix's elements. Return the maximum sum of the matrix's elements using the operation mentioned above.

 

Example 1:

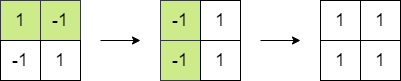
Input: matrix = [[1,-1],[-1,1]]
Output: 4
Explanation: We can follow the following steps to reach sum equals 4:
- Multiply the 2 elements in the first row by -1.
- Multiply the 2 elements in the first column by -1.

Example 2:

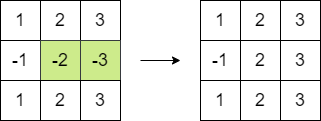
Input: matrix = [[1,2,3],[-1,-2,-3],[1,2,3]]
Output: 16
Explanation: We can follow the following step to reach sum equals 16:
- Multiply the 2 last elements in the second row by -1.

 

Constraints:

• n == matrix.length == matrix[i].length
• 2 <= n <= 250
• -105 <= matrix[i][j] <= 105

 

Solutions

Solution: Greedy

• Time complexity: O(n²)
• Space complexity: O(1)

 

JavaScript

/**
 * @param {number[][]} matrix
 * @return {number}
 */
const maxMatrixSum = function (matrix) {
  const n = matrix.length;
  let result = (negative = 0);
  let min = Number.MAX_SAFE_INTEGER;

  for (let row = 0; row < n; row++) {
    for (let col = 0; col < n; col++) {
      const value = matrix[row][col];

      if (value < 0) negative += 1;
      min = Math.min(Math.abs(value), min);
      result += Math.abs(value);
    }
  }
  const adjustment = negative % 2 ? min * 2 : 0;

  return result - adjustment;
};