1621. Number of Sets of K Non-Overlapping Line Segments

Description

Given n points on a 1-D plane, where the ith point (from 0 to n-1) is at x = i, find the number of ways we can draw exactly k non-overlapping line segments such that each segment covers two or more points. The endpoints of each segment must have integral coordinates. The k line segments do not have to cover all n points, and they are allowed to share endpoints.

Return the number of ways we can draw k non-overlapping line segments. Since this number can be huge, return it modulo 109 + 7.

 

Example 1:

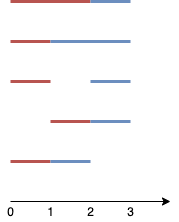
Input: n = 4, k = 2
Output: 5
Explanation: The two line segments are shown in red and blue.
The image above shows the 5 different ways {(0,2),(2,3)}, {(0,1),(1,3)}, {(0,1),(2,3)}, {(1,2),(2,3)}, {(0,1),(1,2)}.

Example 2:

Input: n = 3, k = 1
Output: 3
Explanation: The 3 ways are {(0,1)}, {(0,2)}, {(1,2)}.

Example 3:

Input: n = 30, k = 7
Output: 796297179
Explanation: The total number of possible ways to draw 7 line segments is 3796297200. Taking this number modulo 109 + 7 gives us 796297179.

 

Constraints:

• 2 <= n <= 1000
• 1 <= k <= n-1

 

Solutions

Solution: Combinatorics

• Time complexity: O((n+k−1)(k∗2))
• Space complexity: O((n+k−1)(k∗2))

 

JavaScript

/**
 * @param {number} n
 * @param {number} k
 * @return {number}
 */
const numberOfSets = function (n, k) {
  const MODULO = 10 ** 9 + 7;
  const combinatorics = (n, k) => {
    const dp = new Array(n + 1)
      .fill('')
      .map(_ => new Array(k + 1).fill(1));

    for (let index = 1; index <= n; index++) {
      for (let point = 1; point < index && point <= k; point++) {
        dp[index][point] = (dp[index - 1][point - 1] + dp[index - 1][point]) % MODULO;
      }
    }
    return dp[n][k];
  };

  return combinatorics(n + k - 1, k * 2);
};