3123. Find Edges in Shortest Paths

Description

You are given an undirected weighted graph of n nodes numbered from 0 to n - 1. The graph consists of m edges represented by a 2D array edges, where edges[i] = [ai, bi, wi] indicates that there is an edge between nodes ai and bi with weight wi.

Consider all the shortest paths from node 0 to node n - 1 in the graph. You need to find a boolean array answer where answer[i] is true if the edge edges[i] is part of at least one shortest path. Otherwise, answer[i] is false.

Return the array answer.

Note that the graph may not be connected.

 

Example 1:

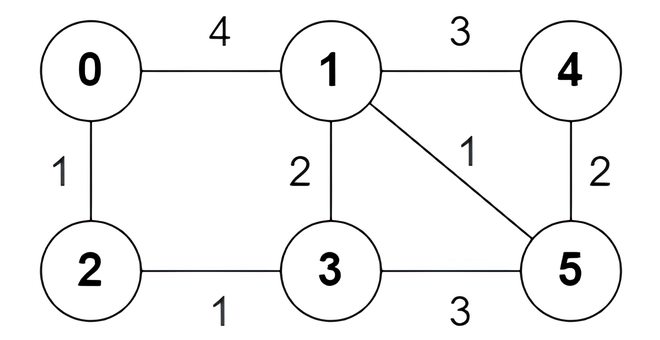
Input: n = 6, edges = [[0,1,4],[0,2,1],[1,3,2],[1,4,3],[1,5,1],[2,3,1],[3,5,3],[4,5,2]]

Output: [true,true,true,false,true,true,true,false]

Explanation:

The following are all the shortest paths between nodes 0 and 5:

• The path 0 -> 1 -> 5: The sum of weights is 4 + 1 = 5.
• The path 0 -> 2 -> 3 -> 5: The sum of weights is 1 + 1 + 3 = 5.
• The path 0 -> 2 -> 3 -> 1 -> 5: The sum of weights is 1 + 1 + 2 + 1 = 5.

Example 2:

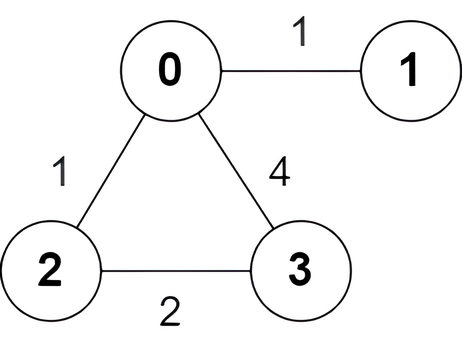
Input: n = 4, edges = [[2,0,1],[0,1,1],[0,3,4],[3,2,2]]

Output: [true,false,false,true]

Explanation:

There is one shortest path between nodes 0 and 3, which is the path 0 -> 2 -> 3 with the sum of weights 1 + 2 = 3.

 

Constraints:

• 2 <= n <= 5 * 104
• m == edges.length
• 1 <= m <= min(5 * 104, n * (n - 1) / 2)
• 0 <= ai, bi < n
• ai != bi
• 1 <= wi <= 105
• There are no repeated edges.

 

Solutions

Solution: Dijkstra's Algorithm

• Time complexity: O((m+n)logn)
• Space complexity: O(m+n)

 

JavaScript

/**
 * @param {number} n
 * @param {number[][]} edges
 * @return {boolean[]}
 */
const findAnswer = function (n, edges) {
  const graph = new Array(n)
    .fill('')
    .map(_ => []);
  const weighteds = new Array(n).fill(Number.MAX_SAFE_INTEGER);
  const queue = new MinPriorityQueue({ priority: ({ weighted }) => weighted });
  const result = Array.from({length: edges.length}).fill(false);

  weighteds[0] = 0;
  queue.enqueue({ node: 0, weighted: 0 });

  for (const [index, [a, b, weighted]] of edges.entries()) {

    graph[a].push({ node: b, weighted, index });
    graph[b].push({ node: a, weighted, index });
  }
  while (!queue.isEmpty()) {
    const { node, weighted } = queue.dequeue().element;

    if (weighted > weighteds[node]) continue;
    for (const to of graph[node]) {
      const totalWeighted = weighted + to.weighted;

      if (totalWeighted >= weighteds[to.node]) continue;
      weighteds[to.node] = totalWeighted;
      queue.enqueue({ node: to.node, weighted: totalWeighted });
    }
  }
  queue.enqueue({ node: n - 1, weighted: weighteds.at(-1) });

  while (!queue.isEmpty()) {
    const { node, weighted } = queue.dequeue().element;

    for (const from of graph[node]) {
      const currentWeighted = weighted - from.weighted;
      const targetWeighted = weighteds[from.node];

      if (currentWeighted !== targetWeighted) continue;
      result[from.index] = true;
      queue.enqueue({ node: from.node, weighted: targetWeighted });
    }
  }
  return result;
};