391. Perfect Rectangle

Description

Given an array rectangles where rectangles[i] = [xi, yi, ai, bi] represents an axis-aligned rectangle. The bottom-left point of the rectangle is (xi, yi) and the top-right point of it is (ai, bi).

Return true if all the rectangles together form an exact cover of a rectangular region.

 

Example 1:

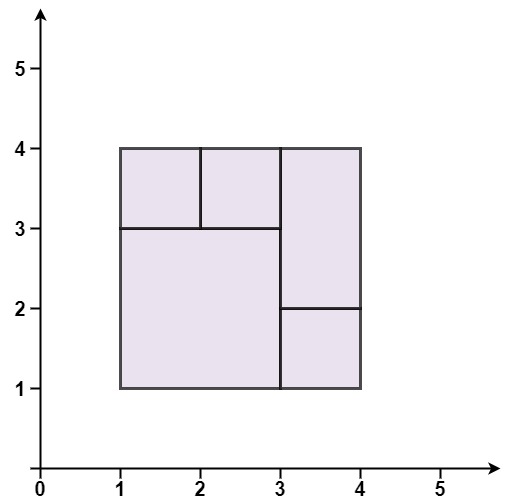
Input: rectangles = [[1,1,3,3],[3,1,4,2],[3,2,4,4],[1,3,2,4],[2,3,3,4]]
Output: true
Explanation: All 5 rectangles together form an exact cover of a rectangular region.

Example 2:

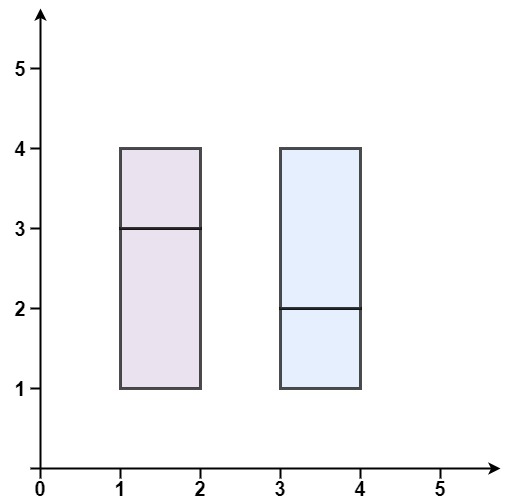
Input: rectangles = [[1,1,2,3],[1,3,2,4],[3,1,4,2],[3,2,4,4]]
Output: false
Explanation: Because there is a gap between the two rectangular regions.

Example 3:

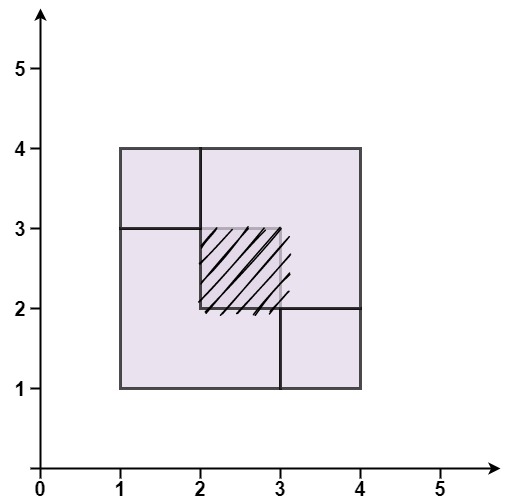
Input: rectangles = [[1,1,3,3],[3,1,4,2],[1,3,2,4],[2,2,4,4]]
Output: false
Explanation: Because two of the rectangles overlap with each other.

 

Constraints:

• 1 <= rectangles.length <= 2 * 104
• rectangles[i].length == 4
• -105 <= xi, yi, ai, bi <= 105

 

Solutions

Solution: Greedy

• Time complexity: O(n)
• Space complexity: O(n)

 

JavaScript

/**
 * @param {number[][]} rectangles
 * @return {boolean}
 */
const isRectangleCover = function (rectangles) {
  const pointSet = new Set();
  let minX = (minY = Number.MAX_SAFE_INTEGER);
  let maxX = (maxY = Number.MIN_SAFE_INTEGER);
  let area = 0;

  for (const [x1, y1, x2, y2] of rectangles) {
    const point1 = `${x1}_${y1}`;
    const point2 = `${x1}_${y2}`;
    const point3 = `${x2}_${y1}`;
    const point4 = `${x2}_${y2}`;

    minX = Math.min(x1, minX);
    minY = Math.min(y1, minY);
    maxX = Math.max(x2, maxX);
    maxY = Math.max(y2, maxY);
    area += (x2 - x1) * (y2 - y1);
    pointSet.has(point1) ? pointSet.delete(point1) : pointSet.add(point1);
    pointSet.has(point2) ? pointSet.delete(point2) : pointSet.add(point2);
    pointSet.has(point3) ? pointSet.delete(point3) : pointSet.add(point3);
    pointSet.has(point4) ? pointSet.delete(point4) : pointSet.add(point4);
  }
  if (pointSet.size !== 4) return false;
  if (!pointSet.has(`${minX}_${minY}`)) return false;
  if (!pointSet.has(`${minX}_${maxY}`)) return false;
  if (!pointSet.has(`${maxX}_${minY}`)) return false;
  if (!pointSet.has(`${maxX}_${maxY}`)) return false;

  return (maxX - minX) * (maxY - minY) === area;
};