1443. Minimum Time to Collect All Apples in a Tree

Description

Given an undirected tree consisting of n vertices numbered from 0 to n-1, which has some apples in their vertices. You spend 1 second to walk over one edge of the tree. Return the minimum time in seconds you have to spend to collect all apples in the tree, starting at vertex 0 and coming back to this vertex.

The edges of the undirected tree are given in the array edges, where edges[i] = [ai, bi] means that exists an edge connecting the vertices ai and bi. Additionally, there is a boolean array hasApple, where hasApple[i] = true means that vertex i has an apple; otherwise, it does not have any apple.

 

Example 1:

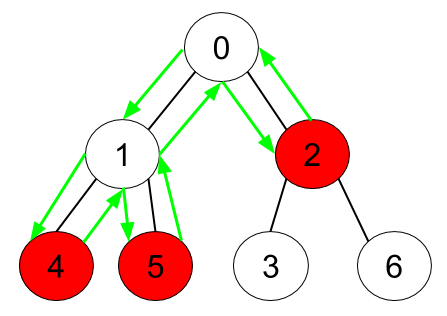
Input: n = 7, edges = [[0,1],[0,2],[1,4],[1,5],[2,3],[2,6]], hasApple = [false,false,true,false,true,true,false]
Output: 8 
Explanation: The figure above represents the given tree where red vertices have an apple. One optimal path to collect all apples is shown by the green arrows.  

Example 2:

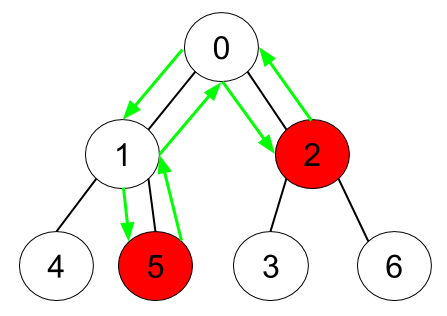
Input: n = 7, edges = [[0,1],[0,2],[1,4],[1,5],[2,3],[2,6]], hasApple = [false,false,true,false,false,true,false]
Output: 6
Explanation: The figure above represents the given tree where red vertices have an apple. One optimal path to collect all apples is shown by the green arrows.  

Example 3:

Input: n = 7, edges = [[0,1],[0,2],[1,4],[1,5],[2,3],[2,6]], hasApple = [false,false,false,false,false,false,false]
Output: 0

 

Constraints:

• 1 <= n <= 105
• edges.length == n - 1
• edges[i].length == 2
• 0 <= ai < bi <= n - 1
• hasApple.length == n

 

Solutions

Solution: Depth-First Search

• Time complexity: O(n)
• Space complexity: O(n)

 

JavaScript

/**
 * @param {number} n
 * @param {number[][]} edges
 * @param {boolean[]} hasApple
 * @return {number}
 */
const minTime = function (n, edges, hasApple) {
  const visited = new Set();
  const edgesMap = edges.reduce((map, [a, b]) => {
    const edgeA = map.get(a) ?? [];
    const edgeB = map.get(b) ?? [];

    edgeA.push(b);
    edgeB.push(a);
    map.set(a, edgeA);
    return map.set(b, edgeB);
  }, new Map());
  const collectApple = (from = 0) => {
    const edges = edgesMap.get(from) ?? [];

    visited.add(from);
    const time = edges.reduce((total, edge) => {
      if (visited.has(edge)) return total;
      return total + collectApple(edge);
    }, 0);

    return time + (from && (hasApple[from] || time) ? 2 : 0);
  };

  return collectApple();
};