407. Trapping Rain Water II

Description

Given an m x n integer matrix heightMap representing the height of each unit cell in a 2D elevation map, return the volume of water it can trap after raining.

 

Example 1:

Input: heightMap = [[1,4,3,1,3,2],[3,2,1,3,2,4],[2,3,3,2,3,1]]
Output: 4
Explanation: After the rain, water is trapped between the blocks.
We have two small ponds 1 and 3 units trapped.
The total volume of water trapped is 4.

Example 2:

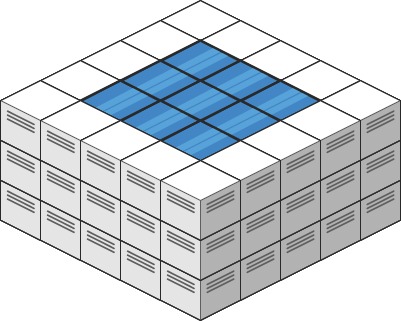
Input: heightMap = [[3,3,3,3,3],[3,2,2,2,3],[3,2,1,2,3],[3,2,2,2,3],[3,3,3,3,3]]
Output: 10

 

Constraints:

• m == heightMap.length
• n == heightMap[i].length
• 1 <= m, n <= 200
• 0 <= heightMap[i][j] <= 2 * 104

 

Solutions

Solution: Breadth-First Search + Priority Queue

• Time complexity: O(mnlogmn)
• Space complexity: O(mn)

 

JavaScript

/**
 * @param {number[][]} heightMap
 * @return {number}
 */
const trapRainWater = function (heightMap) {
  const m = heightMap.length;
  const n = heightMap[0].length;
  const directions = [
    [0, 1],
    [0, -1],
    [1, 0],
    [-1, 0],
  ];
  const queue = new MinPriorityQueue({ priority: ({ height }) => height });
  const visited = new Set();
  let maxHeight = (result = 0);

  for (let row = 0; row < m; row++) {
    for (let col = 0; col < n; col++) {
      if (row > 0 && col > 0 && row !== m - 1 && col !== n - 1) continue;
      queue.enqueue({ height: heightMap[row][col], row, col });
      visited.add(`${row},${col}`);
    }
  }
  while (queue.size()) {
    const cell = queue.dequeue().element;

    maxHeight = Math.max(cell.height, maxHeight);

    for (const [moveRow, moveCol] of directions) {
      const row = cell.row + moveRow;
      const col = cell.col + moveCol;
      const key = `${row},${col}`;

      if (row < 0 || col < 0 || row >= m || col >= n) continue;
      if (visited.has(key)) continue;
      const height = heightMap[row][col];

      visited.add(key);
      result += Math.max(0, maxHeight - height);
      queue.enqueue({ height, row, col });
    }
  }
  return result;
};