124. Binary Tree Maximum Path Sum

Description

A path in a binary tree is a sequence of nodes where each pair of adjacent nodes in the sequence has an edge connecting them. A node can only appear in the sequence at most once. Note that the path does not need to pass through the root.

The path sum of a path is the sum of the node's values in the path.

Given the root of a binary tree, return the maximum path sum of any non-empty path.

 

Example 1:

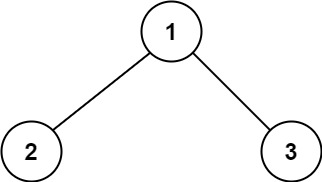
Input: root = [1,2,3]
Output: 6
Explanation: The optimal path is 2 -> 1 -> 3 with a path sum of 2 + 1 + 3 = 6.

Example 2:

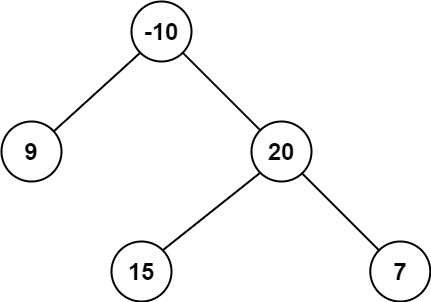
Input: root = [-10,9,20,null,null,15,7]
Output: 42
Explanation: The optimal path is 15 -> 20 -> 7 with a path sum of 15 + 20 + 7 = 42.

 

Constraints:

• The number of nodes in the tree is in the range [1, 3 * 104].
• -1000 <= Node.val <= 1000

 

Solutions

Solution: Depth-First Search

• Time complexity: O(n)
• Space complexity: O(n)

 

JavaScript

/**
 * Definition for a binary tree node.
 * function TreeNode(val, left, right) {
 *     this.val = (val===undefined ? 0 : val)
 *     this.left = (left===undefined ? null : left)
 *     this.right = (right===undefined ? null : right)
 * }
 */
/**
 * @param {TreeNode} root
 * @return {number}
 */
const maxPathSum = function (root) {
  let result = Number.MIN_SAFE_INTEGER;
  const sumPath = (node = root) => {
    if (!node) return 0;
    const { val, left, right } = node;
    const leftSum = val + sumPath(left);
    const rightSum = val + sumPath(right);
    const maxPathSum = Math.max(leftSum, rightSum, val);
    const sum = leftSum + rightSum - val;

    result = Math.max(sum, result, maxPathSum);
    return maxPathSum;
  };

  sumPath();
  return result;
};