1727. Largest Submatrix With Rearrangements

Description

You are given a binary matrix matrix of size m x n, and you are allowed to rearrange the columns of the matrix in any order.

Return the area of the largest submatrix within matrix where every element of the submatrix is 1 after reordering the columns optimally.

 

Example 1:

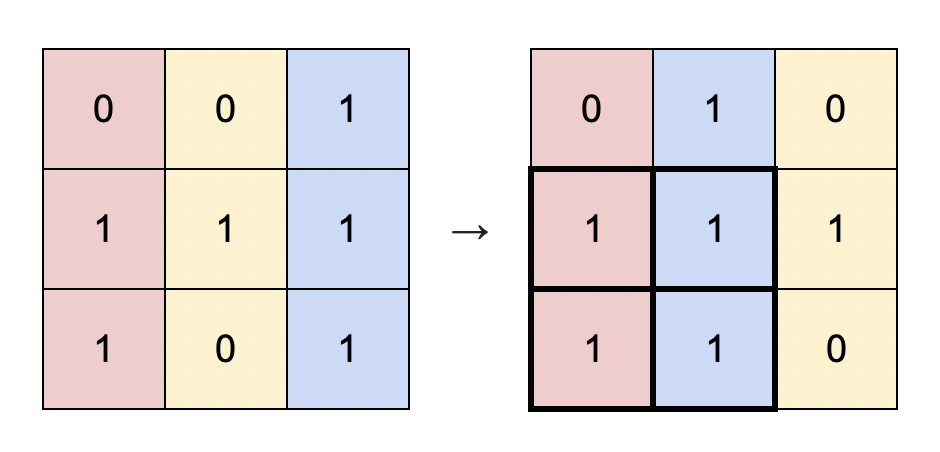
Input: matrix = [[0,0,1],[1,1,1],[1,0,1]]
Output: 4
Explanation: You can rearrange the columns as shown above.
The largest submatrix of 1s, in bold, has an area of 4.

Example 2:

Input: matrix = [[1,0,1,0,1]]
Output: 3
Explanation: You can rearrange the columns as shown above.
The largest submatrix of 1s, in bold, has an area of 3.

Example 3:

Input: matrix = [[1,1,0],[1,0,1]]
Output: 2
Explanation: Notice that you must rearrange entire columns, and there is no way to make a submatrix of 1s larger than an area of 2.

 

Constraints:

• m == matrix.length
• n == matrix[i].length
• 1 <= m * n <= 105
• matrix[i][j] is either 0 or 1.

 

Solutions

Solution: Sorting

• Time complexity: O(m*nlogn)
• Space complexity: O(mn)

 

JavaScript

/**
 * @param {number[][]} matrix
 * @return {number}
 */
const largestSubmatrix = function (matrix) {
  const m = matrix.length;
  const n = matrix[0].length;
  const dp = matrix.map(row => row.map(value => value));
  let result = 0;

  for (let row = 1; row < m; row++) {
    for (let col = 0; col < n; col++) {
      if (!dp[row][col]) continue;
      dp[row][col] += dp[row - 1][col];
    }
  }
  for (let row = 0; row < m; row++) {
    dp[row].sort((a, b) => b - a);

    for (let col = 0; col < n; col++) {
      if (!dp[row][col]) break;
      result = Math.max(dp[row][col] * (col + 1), result);
    }
  }
  return result;
};