1606. Find Servers That Handled Most Number of Requests

Description

You have k servers numbered from 0 to k-1 that are being used to handle multiple requests simultaneously. Each server has infinite computational capacity but cannot handle more than one request at a time. The requests are assigned to servers according to a specific algorithm:

• The ith (0-indexed) request arrives.
• If all servers are busy, the request is dropped (not handled at all).
• If the (i % k)th server is available, assign the request to that server.
• Otherwise, assign the request to the next available server (wrapping around the list of servers and starting from 0 if necessary). For example, if the ith server is busy, try to assign the request to the (i+1)th server, then the (i+2)th server, and so on.

You are given a strictly increasing array arrival of positive integers, where arrival[i] represents the arrival time of the ith request, and another array load, where load[i] represents the load of the ith request (the time it takes to complete). Your goal is to find the busiest server(s). A server is considered busiest if it handled the most number of requests successfully among all the servers.

Return a list containing the IDs (0-indexed) of the busiest server(s). You may return the IDs in any order.

 

Example 1:

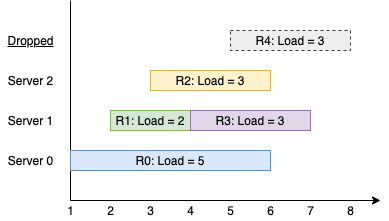
Input: k = 3, arrival = [1,2,3,4,5], load = [5,2,3,3,3] 
Output: [1] 
Explanation: 
All of the servers start out available.
The first 3 requests are handled by the first 3 servers in order.
Request 3 comes in. Server 0 is busy, so it's assigned to the next available server, which is 1.
Request 4 comes in. It cannot be handled since all servers are busy, so it is dropped.
Servers 0 and 2 handled one request each, while server 1 handled two requests. Hence server 1 is the busiest server.

Example 2:

Input: k = 3, arrival = [1,2,3,4], load = [1,2,1,2]
Output: [0]
Explanation: 
The first 3 requests are handled by first 3 servers.
Request 3 comes in. It is handled by server 0 since the server is available.
Server 0 handled two requests, while servers 1 and 2 handled one request each. Hence server 0 is the busiest server.

Example 3:

Input: k = 3, arrival = [1,2,3], load = [10,12,11]
Output: [0,1,2]
Explanation: Each server handles a single request, so they are all considered the busiest.

 

Constraints:

• 1 <= k <= 105
• 1 <= arrival.length, load.length <= 105
• arrival.length == load.length
• 1 <= arrival[i], load[i] <= 109
• arrival is strictly increasing.

 

Solutions

Solution: Priority Queue

• Time complexity: O(nlogk)
• Space complexity: O(n+k)

 

JavaScript

/**
 * @param {number} k
 * @param {number[]} arrival
 * @param {number[]} load
 * @return {number[]}
 */
const busiestServers = function (k, arrival, load) {
  const n = arrival.length;
  const servers = Array.from({ length: k }, () => 0);
  const busyServers = new MinPriorityQueue(({ server, idleTime }) => idleTime || server);
  let beforeModIdleServers = new MinPriorityQueue();
  let afterModIdleServers = new MinPriorityQueue();

  for (let server = 0; server < k; server++) {
    beforeModIdleServers.enqueue(server);
  }

  for (let index = 0; index < n; index++) {
    const time = arrival[index];
    const idleTime = time + load[index];
    const modServer = index % k;

    if (!modServer) {
      afterModIdleServers = beforeModIdleServers;
      beforeModIdleServers = new MinPriorityQueue();
    }

    while (busyServers.size() && busyServers.front().idleTime <= time) {
      const { server } = busyServers.dequeue();

      server < modServer ? beforeModIdleServers.enqueue(server) : afterModIdleServers.enqueue(server);
    }

    while (afterModIdleServers.size() && afterModIdleServers.front() < modServer) {
      const server = afterModIdleServers.dequeue();

      beforeModIdleServers.enqueue(server);
    }

    const server = afterModIdleServers.dequeue() ?? beforeModIdleServers.dequeue();

    if (server === null) continue;

    servers[server] += 1;
    busyServers.enqueue({ server, idleTime });
  }

  const maxRequest = Math.max(...servers);
  const result = [];

  for (let server = 0; server < k; server++) {
    if (servers[server] < maxRequest) continue;

    result.push(server);
  }

  return result;
};