2033. Minimum Operations to Make a Uni-Value Grid

Description

You are given a 2D integer grid of size m x n and an integer x. In one operation, you can add x to or subtract x from any element in the grid.

A uni-value grid is a grid where all the elements of it are equal.

Return the minimum number of operations to make the grid uni-value. If it is not possible, return -1.

 

Example 1:

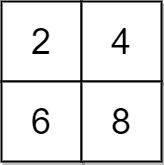
Input: grid = [[2,4],[6,8]], x = 2
Output: 4
Explanation: We can make every element equal to 4 by doing the following: 
- Add x to 2 once.
- Subtract x from 6 once.
- Subtract x from 8 twice.
A total of 4 operations were used.

Example 2:

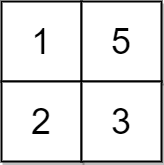
Input: grid = [[1,5],[2,3]], x = 1
Output: 5
Explanation: We can make every element equal to 3.

Example 3:

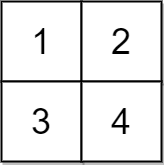
Input: grid = [[1,2],[3,4]], x = 2
Output: -1
Explanation: It is impossible to make every element equal.

 

Constraints:

• m == grid.length
• n == grid[i].length
• 1 <= m, n <= 105
• 1 <= m * n <= 105
• 1 <= x, grid[i][j] <= 104

 

Solutions

Solution: Sorting

• Time complexity: O(mnlogmn)
• Space complexity: O(mn)

 

JavaScript

/**
 * @param {number[][]} grid
 * @param {number} x
 * @return {number}
 */
const minOperations = function (grid, x) {
  const m = grid.length;
  const n = grid[0].length;
  const values = [];
  const remainder = grid[0][0] % x;

  for (let row = 0; row < m; row++) {
    for (let col = 0; col < n; col++) {
      const value = grid[row][col];

      if (value % x !== remainder) return -1;
      values.push(value);
    }
  }
  values.sort((a, b) => a - b);
  const middle = values[Math.floor((m * n) / 2)];

  return values.reduce((result, value) => {
    return result + Math.abs(value - middle) / x;
  }, 0);
};