1697. Checking Existence of Edge Length Limited Paths

Description

An undirected graph of n nodes is defined by edgeList, where edgeList[i] = [ui, vi, disi] denotes an edge between nodes ui and vi with distance disi. Note that there may be multiple edges between two nodes.

Given an array queries, where queries[j] = [pj, qj, limitj], your task is to determine for each queries[j] whether there is a path between pj and qjsuch that each edge on the path has a distance strictly less than limitj .

Return a boolean arrayanswer, where answer.length == queries.length and the jth value of answer is true if there is a path for queries[j] is true, and false otherwise.

 

Example 1:

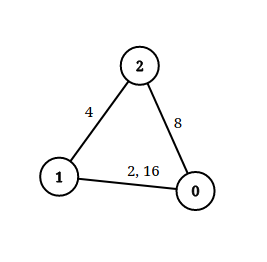
Input: n = 3, edgeList = [[0,1,2],[1,2,4],[2,0,8],[1,0,16]], queries = [[0,1,2],[0,2,5]]
Output: [false,true]
Explanation: The above figure shows the given graph. Note that there are two overlapping edges between 0 and 1 with distances 2 and 16.
For the first query, between 0 and 1 there is no path where each distance is less than 2, thus we return false for this query.
For the second query, there is a path (0 -> 1 -> 2) of two edges with distances less than 5, thus we return true for this query.

Example 2:

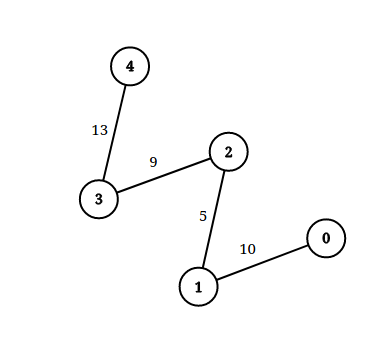
Input: n = 5, edgeList = [[0,1,10],[1,2,5],[2,3,9],[3,4,13]], queries = [[0,4,14],[1,4,13]]
Output: [true,false]
Explanation: The above figure shows the given graph.

 

Constraints:

• 2 <= n <= 105
• 1 <= edgeList.length, queries.length <= 105
• edgeList[i].length == 3
• queries[j].length == 3
• 0 <= ui, vi, pj, qj <= n - 1
• ui != vi
• pj != qj
• 1 <= disi, limitj <= 109
• There may be multiple edges between two nodes.

 

Solutions

Solution: Two Pointers + Union Find

• Time complexity: O(mlogm+eloge)
  • e is edgeList.length
• Space complexity: O(m+n)

 

JavaScript

/**
 * @param {number} n
 * @param {number[][]} edgeList
 * @param {number[][]} queries
 * @return {boolean[]}
 */
const distanceLimitedPathsExist = function (n, edgeList, queries) {
  const m = queries.length;
  const indexedQueries = queries.map((query, index) => ({ query, index }));
  const uf = new UnionFind(n);
  const result = Array.from({ length: m }, () => false);
  let edge = 0;

  edgeList.sort((a, b) => a[2] - b[2]);
  indexedQueries.sort((a, b) => a.query[2] - b.query[2]);

  for (const { query, index } of indexedQueries) {
    const [p, q, limit] = query;

    while (edge < edgeList.length && edgeList[edge][2] < limit) {
      const [u, v] = edgeList[edge];

      uf.union(u, v);
      edge += 1;
    }

    if (uf.find(p) === uf.find(q)) {
      result[index] = true;
    }
  }

  return result;
};

class UnionFind {
  constructor(n) {
    this.groups = Array.from({ length: n }, (_, index) => index);
    this.ranks = Array.from({ length: n }, () => 0);
  }

  find(x) {
    if (this.groups[x] === x) return x;
    const group = this.find(this.groups[x]);

    this.groups[x] = group;

    return group;
  }

  union(x, y) {
    const groupX = this.find(x);
    const groupY = this.find(y);

    if (groupX === groupY) return false;
    if (this.ranks[groupX] > this.ranks[groupY]) {
      this.groups[groupY] = groupX;
    } else if (this.ranks[groupX] < this.ranks[groupY]) {
      this.groups[groupX] = groupY;
    } else {
      this.groups[groupY] = groupX;
      this.ranks[groupX] += 1;
    }

    return true;
  }
}