1504. Count Submatrices With All Ones

Description

Given an m x n binary matrix mat, return the number of submatrices that have all ones.

 

Example 1:

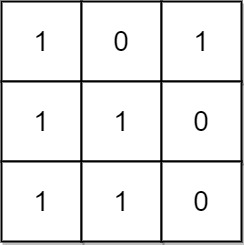
Input: mat = [[1,0,1],[1,1,0],[1,1,0]]
Output: 13
Explanation: 
There are 6 rectangles of side 1x1.
There are 2 rectangles of side 1x2.
There are 3 rectangles of side 2x1.
There is 1 rectangle of side 2x2. 
There is 1 rectangle of side 3x1.
Total number of rectangles = 6 + 2 + 3 + 1 + 1 = 13.

Example 2:

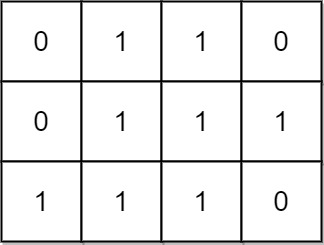
Input: mat = [[0,1,1,0],[0,1,1,1],[1,1,1,0]]
Output: 24
Explanation: 
There are 8 rectangles of side 1x1.
There are 5 rectangles of side 1x2.
There are 2 rectangles of side 1x3. 
There are 4 rectangles of side 2x1.
There are 2 rectangles of side 2x2. 
There are 2 rectangles of side 3x1. 
There is 1 rectangle of side 3x2. 
Total number of rectangles = 8 + 5 + 2 + 4 + 2 + 2 + 1 = 24.

 

Constraints:

• 1 <= m, n <= 150
• mat[i][j] is either 0 or 1.

 

Solutions

Solution: Dynamic Programming + Stack

• Time complexity: O(mn)
• Space complexity: O(n)

 

JavaScript

/**
 * @param {number[][]} mat
 * @return {number}
 */
const numSubmat = function (mat) {
  const m = mat.length;
  const n = mat[0].length;
  const cols = Array.from({ length: n }, () => 0);
  let result = 0;

  const countSubmat = () => {
    const submat = new Array(n).fill(0);
    const stack = [];

    for (let col = 0; col < n; col++) {
      while (stack.length && cols[stack.at(-1)] >= cols[col]) {
        stack.pop();
      }

      if (stack.length) {
        const prev = stack.at(-1);

        submat[col] = submat[prev] + cols[col] * (col - prev);
      } else {
        submat[col] = cols[col] * (col + 1);
      }

      stack.push(col);
    }

    return submat.reduce((result, count) => result + count);
  };

  for (let row = 0; row < m; row++) {
    for (let col = 0; col < n; col++) {
      cols[col] = mat[row][col] ? cols[col] + 1 : 0;
    }

    result += countSubmat();
  }

  return result;
};