1388. Pizza With 3n Slices

Description

There is a pizza with 3n slices of varying size, you and your friends will take slices of pizza as follows:

• You will pick any pizza slice.
• Your friend Alice will pick the next slice in the anti-clockwise direction of your pick.
• Your friend Bob will pick the next slice in the clockwise direction of your pick.
• Repeat until there are no more slices of pizzas.

Given an integer array slices that represent the sizes of the pizza slices in a clockwise direction, return the maximum possible sum of slice sizes that you can pick.

 

Example 1:

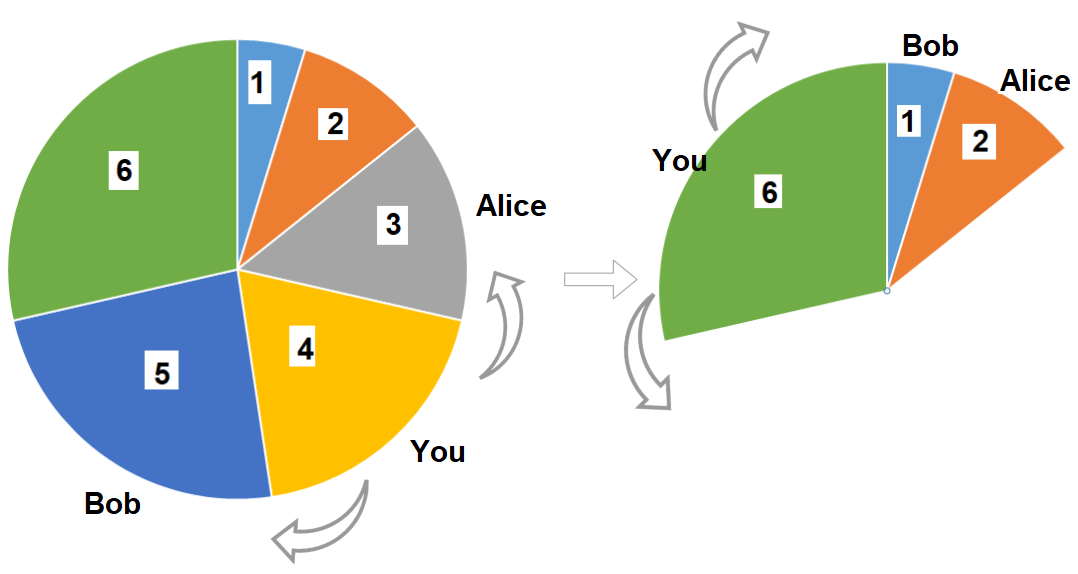
Input: slices = [1,2,3,4,5,6]
Output: 10
Explanation: Pick pizza slice of size 4, Alice and Bob will pick slices with size 3 and 5 respectively. Then Pick slices with size 6, finally Alice and Bob will pick slice of size 2 and 1 respectively. Total = 4 + 6.

Example 2:

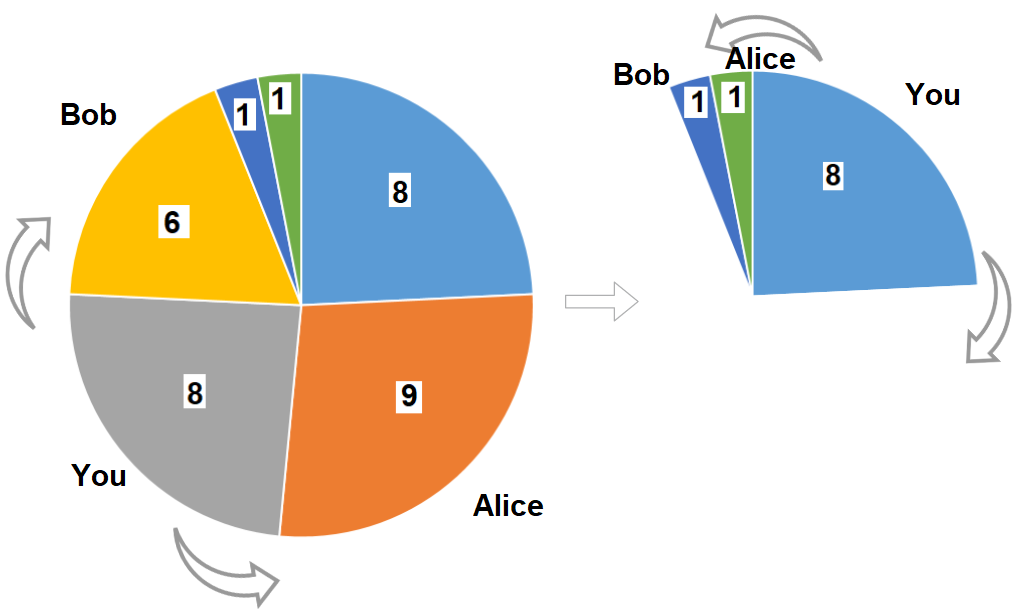
Input: slices = [8,9,8,6,1,1]
Output: 16
Explanation: Pick pizza slice of size 8 in each turn. If you pick slice with size 9 your partners will pick slices of size 8.

 

Constraints:

• 3 * n == slices.length
• 1 <= slices.length <= 500
• 1 <= slices[i] <= 1000

 

Solutions

Solution: Dynamic Programming

• Time complexity: O(nk)
• Space complexity: O(nk + k)

 

JavaScript

/**
 * @param {number[]} slices
 * @return {number}
 */
const maxSizeSlices = function (slices) {
  const n = slices.length;
  const k = n / 3;

  const pickPizza = (index, end, groups, dp) => {
    if (end - index < groups * 2 - 1) return Number.MIN_SAFE_INTEGER;

    if (groups === 1) {
      return Math.max(...slices.slice(index, end));
    }

    if (dp[index][groups]) return dp[index][groups];
    const pick = slices[index] + pickPizza(index + 2, end, groups - 1, dp);
    const unPick = pickPizza(index + 1, end, groups, dp);
    const result = Math.max(pick, unPick);

    dp[index][groups] = result;

    return result;
  };

  const dp1 = Array.from({ length: n }, () => new Array(k + 1).fill(0));
  const dp2 = Array.from({ length: n }, () => new Array(k + 1).fill(0));
  const startFirst = pickPizza(0, n - 1, k, dp1);
  const startSecond = pickPizza(1, n, k, dp2);

  return Math.max(startFirst, startSecond);
};