1719. Number Of Ways To Reconstruct A Tree

Description

You are given an array pairs, where pairs[i] = [xi, yi], and:

• There are no duplicates.
• xi < yi

Let ways be the number of rooted trees that satisfy the following conditions:

• The tree consists of nodes whose values appeared in pairs.
• A pair [xi, yi] exists in pairs if and only if xi is an ancestor of yi or yi is an ancestor of xi.
• Note: the tree does not have to be a binary tree.

Two ways are considered to be different if there is at least one node that has different parents in both ways.

Return:

• 0 if ways == 0
• 1 if ways == 1
• 2 if ways > 1

A rooted tree is a tree that has a single root node, and all edges are oriented to be outgoing from the root.

An ancestor of a node is any node on the path from the root to that node (excluding the node itself). The root has no ancestors.

 

Example 1:

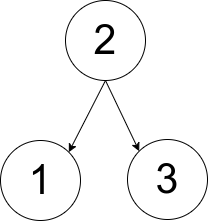
Input: pairs = [[1,2],[2,3]]
Output: 1
Explanation: There is exactly one valid rooted tree, which is shown in the above figure.

Example 2:

Input: pairs = [[1,2],[2,3],[1,3]]
Output: 2
Explanation: There are multiple valid rooted trees. Three of them are shown in the above figures.

Example 3:

Input: pairs = [[1,2],[2,3],[2,4],[1,5]]
Output: 0
Explanation: There are no valid rooted trees.

 

Constraints:

• 1 <= pairs.length <= 105
• 1 <= xi < yi <= 500
• The elements in pairs are unique.

 

Solutions

Solution: Depth-First Search

• Time complexity: O(n+m²logm)
• Space complexity: O(m²)

 

JavaScript

/**
 * @param {number[][]} pairs
 * @return {number}
 */
const checkWays = function (pairs) {
  const graph = new Map();

  for (const [x, y] of pairs) {
    if (!graph.has(x)) graph.set(x, []);
    if (!graph.has(y)) graph.set(y, []);

    graph.get(x).push(y);
    graph.get(y).push(x);
  }

  const m = Math.max(...graph.keys());
  const indegree = Array.from({ length: m + 1 }, () => 0);
  const connected = Array.from({ length: m + 1 }, () => {
    return Array.from({ length: m + 1 }, () => false);
  });

  for (const [x, y] of pairs) {
    indegree[x] += 1;
    indegree[y] += 1;
    connected[x][y] = true;
    connected[y][x] = true;
  }

  const root = indegree.indexOf(graph.size - 1);

  if (root === -1) return 0;
  const visited = Array.from({ length: m + 1 }, () => false);
  const ancestors = [];
  let multipleWays = false;

  for (const nodes of graph.values()) {
    nodes.sort((a, b) => indegree[b] - indegree[a]);
  }

  const isReconstructTree = node => {
    const isConnected = ancestors.every(ancestor => connected[ancestor][node]);

    visited[node] = true;

    if (!isConnected) return false;

    ancestors.push(node);

    for (const neighbor of graph.get(node)) {
      if (visited[neighbor]) continue;
      if (indegree[node] === indegree[neighbor]) {
        multipleWays = true;
      }
      if (!isReconstructTree(neighbor)) return false;
    }

    ancestors.pop();

    return true;
  };

  if (!isReconstructTree(root)) return 0;

  return multipleWays ? 2 : 1;
};