1931. Painting a Grid With Three Different Colors

Description

You are given two integers m and n. Consider an m x n grid where each cell is initially white. You can paint each cell red, green, or blue. All cells must be painted.

Return the number of ways to color the grid with no two adjacent cells having the same color. Since the answer can be very large, return it modulo 109 + 7.

 

Example 1:

Input: m = 1, n = 1
Output: 3
Explanation: The three possible colorings are shown in the image above.

Example 2:

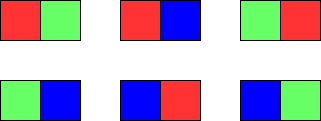
Input: m = 1, n = 2
Output: 6
Explanation: The six possible colorings are shown in the image above.

Example 3:

Input: m = 5, n = 5
Output: 580986

 

Constraints:

• 1 <= m <= 5
• 1 <= n <= 1000

 

Solutions

Solution: Dynamic Programming

• Time complexity: O(n*2^2m*3^m)
• Space complexity: O(n*2^2m)

 

JavaScript

/**
 * @param {number} m
 * @param {number} n
 * @return {number}
 */
const colorTheGrid = function (m, n) {
  const MODULO = BigInt(10 ** 9 + 7);
  const dp = Array.from({ length: n }, () => new Array(2 ** (m * 2)).fill(0));

  const getColor = (row, mask) => {
    return (mask >> (row * 2)) & 3;
  };

  const fillColor = (row, col, prevMask, colorMask) => {
    if (col === n) return 1n;
    if (dp[col][prevMask]) return dp[col][prevMask];
    if (row === m) return fillColor(0, col + 1, colorMask, 0);
    let result = 0n;

    for (let color = 1; color <= 3; color++) {
      if (getColor(row, prevMask) === color) continue;
      if (row && getColor(row - 1, colorMask) === color) continue;
      const nextColorMask = colorMask | (color << (row * 2));

      result = (result + fillColor(row + 1, col, prevMask, nextColorMask)) % MODULO;
    }

    if (row === 0) {
      dp[col][prevMask] = result;
    }

    return result;
  };

  return Number(fillColor(0, 0, 0, 0));
};