3562. Maximum Profit from Trading Stocks with Discounts

Description

You are given an integer n, representing the number of employees in a company. Each employee is assigned a unique ID from 1 to n, and employee 1 is the CEO. You are given two 1-based integer arrays, present and future, each of length n, where:

• present[i] represents the current price at which the ith employee can buy a stock today.
• future[i] represents the expected price at which the ith employee can sell the stock tomorrow.

The company's hierarchy is represented by a 2D integer array hierarchy, where hierarchy[i] = [ui, vi] means that employee ui is the direct boss of employee vi.

Additionally, you have an integer budget representing the total funds available for investment.

However, the company has a discount policy: if an employee's direct boss purchases their own stock, then the employee can buy their stock at half the original price (floor(present[v] / 2)).

Return the maximum profit that can be achieved without exceeding the given budget.

Note:

• You may buy each stock at most once.
• You cannot use any profit earned from future stock prices to fund additional investments and must buy only from budget.

 

Example 1:

Input: n = 2, present = [1,2], future = [4,3], hierarchy = [[1,2]], budget = 3

Output: 5

Explanation:

• Employee 1 buys the stock at price 1 and earns a profit of 4 - 1 = 3.
• Since Employee 1 is the direct boss of Employee 2, Employee 2 gets a discounted price of floor(2 / 2) = 1.
• Employee 2 buys the stock at price 1 and earns a profit of 3 - 1 = 2.
• The total buying cost is 1 + 1 = 2 <= budget. Thus, the maximum total profit achieved is 3 + 2 = 5.

Example 2:

Input: n = 2, present = [3,4], future = [5,8], hierarchy = [[1,2]], budget = 4

Output: 4

Explanation:

• Employee 2 buys the stock at price 4 and earns a profit of 8 - 4 = 4.
• Since both employees cannot buy together, the maximum profit is 4.

Example 3:

Input: n = 3, present = [4,6,8], future = [7,9,11], hierarchy = [[1,2],[1,3]], budget = 10

Output: 10

Explanation:

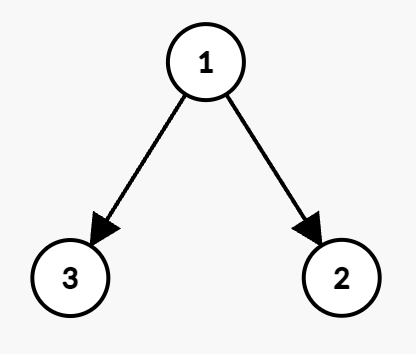
• Employee 1 buys the stock at price 4 and earns a profit of 7 - 4 = 3.
• Employee 3 would get a discounted price of floor(8 / 2) = 4 and earns a profit of 11 - 4 = 7.
• Employee 1 and Employee 3 buy their stocks at a total cost of 4 + 4 = 8 <= budget. Thus, the maximum total profit achieved is 3 + 7 = 10.

Example 4:

Input: n = 3, present = [5,2,3], future = [8,5,6], hierarchy = [[1,2],[2,3]], budget = 7

Output: 12

Explanation:

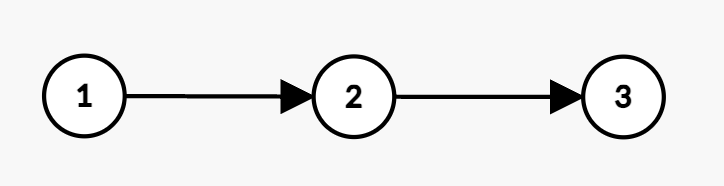
• Employee 1 buys the stock at price 5 and earns a profit of 8 - 5 = 3.
• Employee 2 would get a discounted price of floor(2 / 2) = 1 and earns a profit of 5 - 1 = 4.
• Employee 3 would get a discounted price of floor(3 / 2) = 1 and earns a profit of 6 - 1 = 5.
• The total cost becomes 5 + 1 + 1 = 7 <= budget. Thus, the maximum total profit achieved is 3 + 4 + 5 = 12.

 

Constraints:

• 1 <= n <= 160
• present.length, future.length == n
• 1 <= present[i], future[i] <= 50
• hierarchy.length == n - 1
• hierarchy[i] == [ui, vi]
• 1 <= ui, vi <= n
• ui != vi
• 1 <= budget <= 160
• There are no duplicate edges.
• Employee 1 is the direct or indirect boss of every employee.
• The input graph hierarchy is guaranteed to have no cycles.

 

Solutions

Solution: Dynamic Programming

• Time complexity: O(n*budget²)
• Space complexity: O(n*budget)

 

JavaScript

/**
 * @param {number} n
 * @param {number[]} present
 * @param {number[]} future
 * @param {number[][]} hierarchy
 * @param {number} budget
 * @return {number}
 */
const maxProfit = function (n, present, future, hierarchy, budget) {
  const graph = Array.from({ length: n }, () => []);
  const memo = Array.from({ length: n }, () => [null, null]);

  for (const [u, v] of hierarchy) {
    graph[u - 1].push(v - 1);
  }

  const mergeDp = (a, b) => {
    const result = new Array(budget + 1).fill(Number.MIN_SAFE_INTEGER);

    for (let costA = 0; costA <= budget; costA++) {
      if (a[costA] === Number.MIN_SAFE_INTEGER) continue;

      for (let costB = 0; costB <= budget; costB++) {
        if (b[costB] === Number.MIN_SAFE_INTEGER) continue;

        const cost = costA + costB;

        if (cost > budget) continue;

        const profit = a[costA] + b[costB];

        result[cost] = Math.max(result[cost], profit);
      }
    }

    return result;
  };

  const tradingStock = (employee, bossBought) => {
    const bought = bossBought ? 1 : 0;

    if (memo[employee][bought]) return memo[employee][bought];

    const cost = present[employee];
    const discountCost = Math.floor(cost / 2);
    const realCost = bossBought ? discountCost : cost;
    const profit = future[employee] - realCost;
    let dp = new Array(budget + 1).fill(Number.MIN_SAFE_INTEGER);
    let skipDp = new Array(budget + 1).fill(Number.MIN_SAFE_INTEGER);

    skipDp[0] = 0;

    for (const sub of graph[employee]) {
      const subDp = tradingStock(sub, false);

      skipDp = mergeDp(subDp, skipDp);
    }

    if (realCost <= budget) {
      dp[realCost] = profit;

      for (const sub of graph[employee]) {
        const subDp = tradingStock(sub, true);

        dp = mergeDp(subDp, dp);
      }
    }

    const result = new Array(budget + 1).fill(Number.MIN_SAFE_INTEGER);

    for (let index = 0; index <= budget; index++) {
      result[index] = Math.max(dp[index], skipDp[index]);
    }

    memo[employee][bought] = result;

    return result;
  };

  const dp = tradingStock(0, false);

  return Math.max(...dp);
};