3454. Separate Squares II

Description

You are given a 2D integer array squares. Each squares[i] = [xi, yi, li] represents the coordinates of the bottom-left point and the side length of a square parallel to the x-axis.

Find the minimum y-coordinate value of a horizontal line such that the total area covered by squares above the line equals the total area covered by squares below the line.

Answers within 10-5 of the actual answer will be accepted.

Note: Squares may overlap. Overlapping areas should be counted only once in this version.

 

Example 1:

Input: squares = [[0,0,1],[2,2,1]]

Output: 1.00000

Explanation:

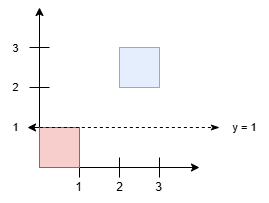
Any horizontal line between y = 1 and y = 2 results in an equal split, with 1 square unit above and 1 square unit below. The minimum y-value is 1.

Example 2:

Input: squares = [[0,0,2],[1,1,1]]

Output: 1.00000

Explanation:

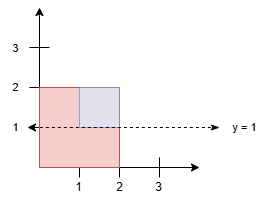
Since the blue square overlaps with the red square, it will not be counted again. Thus, the line y = 1 splits the squares into two equal parts.

 

Constraints:

• 1 <= squares.length <= 5 * 104
• squares[i] = [xi, yi, li]
• squares[i].length == 3
• 0 <= xi, yi <= 109
• 1 <= li <= 109
• The total area of all the squares will not exceed 1015.

 

Solutions

Solution: Line Sweep + Segment Tree

• Time complexity: O(nlogn)
• Space complexity: O(n)

 

JavaScript

/**
 * @param {number[][]} squares
 * @return {number}
 */
const separateSquares = function (squares) {
  const events = [];
  const xSet = new Set();

  for (const [xl, y, l] of squares) {
    const xr = xl + l;

    events.push({ y, delta: 1, xl, xr }, { y: y + l, delta: -1, xl, xr });
    xSet.add(xl);
    xSet.add(xr);
  }

  events.sort((a, b) => a.y - b.y);

  const xs = [...xSet].toSorted((a, b) => a - b);
  const halfArea = getTotalArea(events, xs) / 2;
  const tree = new SegmentTree(xs);
  let prevY = 0;
  let area = 0;

  for (const { y, xl, xr, delta } of events) {
    const coveredWidth = tree.getCoveredWidth();
    const currentArea = (y - prevY) * coveredWidth;

    if (area + currentArea >= halfArea) {
      const rest = halfArea - area;

      return prevY + rest / coveredWidth;
    }

    tree.add(xl, xr, delta);
    prevY = y;
    area += currentArea;
  }

  return -1;
};

function getTotalArea(events, xs) {
  const tree = new SegmentTree(xs);
  let prevY = 0;
  let area = 0;

  for (const { y, xl, xr, delta } of events) {
    area += (y - prevY) * tree.getCoveredWidth();
    tree.add(xl, xr, delta);
    prevY = y;
  }

  return area;
}

class SegmentTree {
  constructor(xs) {
    this.xs = xs;
    this.n = xs.length - 1;
    this.coveredCount = new Array(this.n * 4).fill(0);
    this.coveredWidth = new Array(this.n * 4).fill(0);
  }

  add(xl, xr, delta) {
    this.#add(0, 0, this.n - 1, xl, xr, delta);
  }

  #add(index, low, high, xl, xr, delta) {
    if (this.xs[low] >= xr || this.xs[high + 1] <= xl) return;

    if (this.xs[low] >= xl && this.xs[high + 1] <= xr) {
      this.coveredCount[index] += delta;
    } else {
      const mid = Math.floor((low + high) / 2);

      this.#add(index * 2 + 1, low, mid, xl, xr, delta);
      this.#add(index * 2 + 2, mid + 1, high, xl, xr, delta);
    }

    if (this.coveredCount[index] > 0) {
      this.coveredWidth[index] = this.xs[high + 1] - this.xs[low];
    } else if (low === high) {
      this.coveredWidth[index] = 0;
    } else {
      this.coveredWidth[index] = this.coveredWidth[index * 2 + 1] + this.coveredWidth[index * 2 + 2];
    }
  }

  getCoveredWidth() {
    return this.coveredWidth[0];
  }
}