865. Smallest Subtree with all the Deepest Nodes

Description

Given the root of a binary tree, the depth of each node is the shortest distance to the root.

Return the smallest subtree such that it contains all the deepest nodes in the original tree.

A node is called the deepest if it has the largest depth possible among any node in the entire tree.

The subtree of a node is a tree consisting of that node, plus the set of all descendants of that node.

 

Example 1:

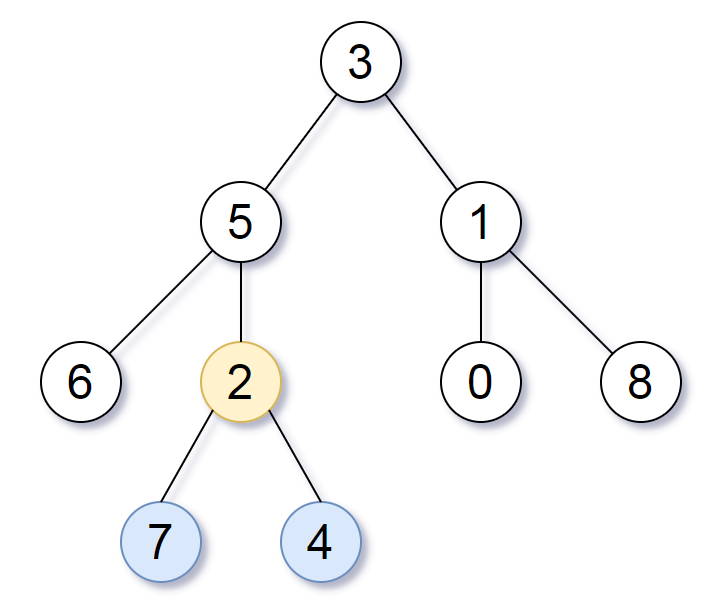
Input: root = [3,5,1,6,2,0,8,null,null,7,4]
Output: [2,7,4]
Explanation: We return the node with value 2, colored in yellow in the diagram.
The nodes coloured in blue are the deepest nodes of the tree.
Notice that nodes 5, 3 and 2 contain the deepest nodes in the tree but node 2 is the smallest subtree among them, so we return it.

Example 2:

Input: root = [1]
Output: [1]
Explanation: The root is the deepest node in the tree.

Example 3:

Input: root = [0,1,3,null,2]
Output: [2]
Explanation: The deepest node in the tree is 2, the valid subtrees are the subtrees of nodes 2, 1 and 0 but the subtree of node 2 is the smallest.

 

Constraints:

• The number of nodes in the tree will be in the range [1, 500].
• 0 <= Node.val <= 500
• The values of the nodes in the tree are unique.

 

Note: This question is the same as 1123: https://leetcode.com/problems/lowest-common-ancestor-of-deepest-leaves/

 

Solutions

Solution: Depth-First Search

• Time complexity: O(n)
• Space complexity: O(h)

 

JavaScript

/**
 * Definition for a binary tree node.
 * function TreeNode(val, left, right) {
 *     this.val = (val===undefined ? 0 : val)
 *     this.left = (left===undefined ? null : left)
 *     this.right = (right===undefined ? null : right)
 * }
 */
/**
 * @param {TreeNode} root
 * @return {TreeNode}
 */
const subtreeWithAllDeepest = function (root) {
  const dfsTree = node => {
    if (!node) return { node: null, deep: 0 };

    const left = dfsTree(node.left);
    const right = dfsTree(node.right);

    if (left.deep > right.deep) {
      return { node: left.node, deep: left.deep + 1 };
    }

    if (right.deep > left.deep) {
      return { node: right.node, deep: right.deep + 1 };
    }

    return { node, deep: left.deep + 1 };
  };

  return dfsTree(root).node;
};