2392. Build a Matrix With Conditions

Description

You are given a positive integer k. You are also given:

• a 2D integer array rowConditions of size n where rowConditions[i] = [abovei, belowi], and
• a 2D integer array colConditions of size m where colConditions[i] = [lefti, righti].

The two arrays contain integers from 1 to k.

You have to build a k x k matrix that contains each of the numbers from 1 to k exactly once. The remaining cells should have the value 0.

The matrix should also satisfy the following conditions:

• The number abovei should appear in a row that is strictly above the row at which the number belowi appears for all i from 0 to n - 1.
• The number lefti should appear in a column that is strictly left of the column at which the number righti appears for all i from 0 to m - 1.

Return any matrix that satisfies the conditions. If no answer exists, return an empty matrix.

 

Example 1:

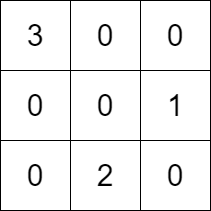
Input: k = 3, rowConditions = [[1,2],[3,2]], colConditions = [[2,1],[3,2]]
Output: [[3,0,0],[0,0,1],[0,2,0]]
Explanation: The diagram above shows a valid example of a matrix that satisfies all the conditions.
The row conditions are the following:
- Number 1 is in row 1, and number 2 is in row 2, so 1 is above 2 in the matrix.
- Number 3 is in row 0, and number 2 is in row 2, so 3 is above 2 in the matrix.
The column conditions are the following:
- Number 2 is in column 1, and number 1 is in column 2, so 2 is left of 1 in the matrix.
- Number 3 is in column 0, and number 2 is in column 1, so 3 is left of 2 in the matrix.
Note that there may be multiple correct answers.

Example 2:

Input: k = 3, rowConditions = [[1,2],[2,3],[3,1],[2,3]], colConditions = [[2,1]]
Output: []
Explanation: From the first two conditions, 3 has to be below 1 but the third conditions needs 3 to be above 1 to be satisfied.
No matrix can satisfy all the conditions, so we return the empty matrix.

 

Constraints:

• 2 <= k <= 400
• 1 <= rowConditions.length, colConditions.length <= 104
• rowConditions[i].length == colConditions[i].length == 2
• 1 <= abovei, belowi, lefti, righti <= k
• abovei != belowi
• lefti != righti

 

Solutions

Solution: Topological Sort

• Time complexity: O(m+n+k)
• Space complexity: O(m+n+k²)

 

JavaScript

/**
 * @param {number} k
 * @param {number[][]} rowConditions
 * @param {number[][]} colConditions
 * @return {number[][]}
 */
const buildMatrix = function (k, rowConditions, colConditions) {
  const topologicalSort = conditions => {
    const indegree = Array.from({ length: k + 1 }, () => 0);
    const graph = Array.from({ length: k + 1 }, () => []);
    const order = [];
    let queue = [];

    for (const [u, v] of conditions) {
      indegree[v] += 1;
      graph[u].push(v);
    }

    for (let index = 1; index <= k; index++) {
      if (indegree[index]) continue;

      queue.push(index);
      order.push(index);
    }

    while (queue.length) {
      const nextQueue = [];

      for (const node of queue) {
        for (const next of graph[node]) {
          indegree[next] -= 1;

          if (indegree[next]) continue;

          nextQueue.push(next);
          order.push(next);
        }
      }

      queue = nextQueue;
    }

    return order.length < k ? null : order;
  };

  const rowOrder = topologicalSort(rowConditions);

  if (!rowOrder) return [];

  const colOrder = topologicalSort(colConditions);

  if (!colOrder) return [];

  const rowIndices = Array.from({ length: k + 1 }, () => 0);
  const result = Array.from({ length: k }, () => new Array(k).fill(0));

  for (let row = 0; row < k; row++) {
    const num = rowOrder[row];

    rowIndices[num] = row;
  }

  for (let col = 0; col < k; col++) {
    const num = colOrder[col];
    const row = rowIndices[num];

    result[row][col] = num;
  }

  return result;
};