2328. Number of Increasing Paths in a Grid

Description

You are given an m x n integer matrix grid, where you can move from a cell to any adjacent cell in all 4 directions.

Return the number of strictly increasing paths in the grid such that you can start from any cell and end at any cell. Since the answer may be very large, return it modulo 109 + 7.

Two paths are considered different if they do not have exactly the same sequence of visited cells.

 

Example 1:

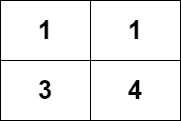
Input: grid = [[1,1],[3,4]]
Output: 8
Explanation: The strictly increasing paths are:
- Paths with length 1: [1], [1], [3], [4].
- Paths with length 2: [1 -> 3], [1 -> 4], [3 -> 4].
- Paths with length 3: [1 -> 3 -> 4].
The total number of paths is 4 + 3 + 1 = 8.

Example 2:

Input: grid = [[1],[2]]
Output: 3
Explanation: The strictly increasing paths are:
- Paths with length 1: [1], [2].
- Paths with length 2: [1 -> 2].
The total number of paths is 2 + 1 = 3.

 

Constraints:

• m == grid.length
• n == grid[i].length
• 1 <= m, n <= 1000
• 1 <= m * n <= 105
• 1 <= grid[i][j] <= 105

 

Solutions

Solution: Dynamic Programming

• Time complexity: O(mn)
• Space complexity: O(mn)

 

JavaScript

/**
 * @param {number[][]} grid
 * @return {number}
 */
const countPaths = function (grid) {
  const MODULO = 10 ** 9 + 7;
  const m = grid.length;
  const n = grid[0].length;
  const directions = [
    [0, 1],
    [0, -1],
    [1, 0],
    [-1, 0],
  ];
  const dp = Array.from({ length: m }, () => new Array(n).fill(0));
  let result = 0;

  const increasingPaths = (row, col) => {
    if (dp[row][col]) return dp[row][col];

    const current = grid[row][col];
    let paths = 1;

    for (const [moveRow, moveCol] of directions) {
      const nextRow = row + moveRow;
      const nextCol = col + moveCol;

      if (nextRow < 0 || nextCol < 0 || nextRow >= m || nextCol >= n) continue;
      if (current >= grid[nextRow][nextCol]) continue;

      paths = (paths + increasingPaths(nextRow, nextCol)) % MODULO;
    }

    dp[row][col] = paths;

    return paths;
  };

  for (let row = 0; row < m; row++) {
    for (let col = 0; col < n; col++) {
      result = (result + increasingPaths(row, col)) % MODULO;
    }
  }

  return result;
};