2242. Maximum Score of a Node Sequence

Description

There is an undirected graph with n nodes, numbered from 0 to n - 1.

You are given a 0-indexed integer array scores of length n where scores[i] denotes the score of node i. You are also given a 2D integer array edges where edges[i] = [ai, bi] denotes that there exists an undirected edge connecting nodes ai and bi.

A node sequence is valid if it meets the following conditions:

• There is an edge connecting every pair of adjacent nodes in the sequence.
• No node appears more than once in the sequence.

The score of a node sequence is defined as the sum of the scores of the nodes in the sequence.

Return the maximum score of a valid node sequence with a length of 4. If no such sequence exists, return-1.

 

Example 1:

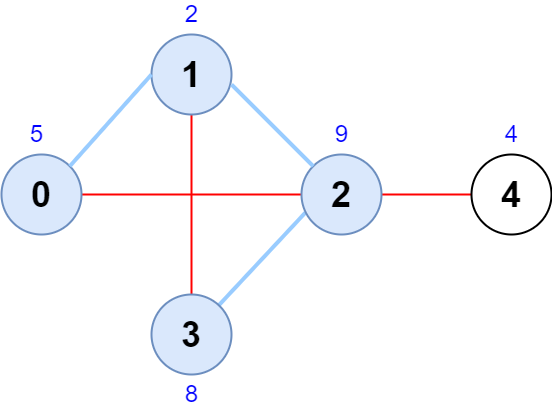
Input: scores = [5,2,9,8,4], edges = [[0,1],[1,2],[2,3],[0,2],[1,3],[2,4]]
Output: 24
Explanation: The figure above shows the graph and the chosen node sequence [0,1,2,3].
The score of the node sequence is 5 + 2 + 9 + 8 = 24.
It can be shown that no other node sequence has a score of more than 24.
Note that the sequences [3,1,2,0] and [1,0,2,3] are also valid and have a score of 24.
The sequence [0,3,2,4] is not valid since no edge connects nodes 0 and 3.

Example 2:

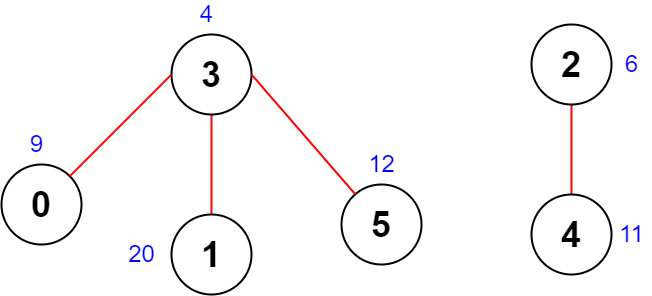
Input: scores = [9,20,6,4,11,12], edges = [[0,3],[5,3],[2,4],[1,3]]
Output: -1
Explanation: The figure above shows the graph.
There are no valid node sequences of length 4, so we return -1.

 

Constraints:

• n == scores.length
• 4 <= n <= 5 * 104
• 1 <= scores[i] <= 108
• 0 <= edges.length <= 5 * 104
• edges[i].length == 2
• 0 <= ai, bi <= n - 1
• ai != bi
• There are no duplicate edges.

 

Solutions

Solution: Greedy

• Time complexity: O(nlogn)
• Space complexity: O(n)

 

JavaScript

/**
 * @param {number[]} scores
 * @param {number[][]} edges
 * @return {number}
 */
const maximumScore = function (scores, edges) {
  const n = scores.length;
  const graph = Array.from({ length: n }, () => []);
  let result = -1;

  for (const [a, b] of edges) {
    graph[a].push(b);
    graph[b].push(a);
  }

  for (let node = 0; node < n; node++) {
    const neighbors = graph[node];

    neighbors.sort((a, b) => scores[b] - scores[a]);
    graph[node] = neighbors.slice(0, 3);
  }

  for (const [a, b] of edges) {
    for (const c of graph[a]) {
      if (a === c || b === c) continue;

      for (const d of graph[b]) {
        if (d === c || d === a || d === b) continue;

        const sum = scores[a] + scores[b] + scores[c] + scores[d];

        result = Math.max(sum, result);
      }
    }
  }

  return result;
};