3650. Minimum Cost Path with Edge Reversals

Description

You are given a directed, weighted graph with n nodes labeled from 0 to n - 1, and an array edges where edges[i] = [ui, vi, wi] represents a directed edge from node ui to node vi with cost wi.

Each node ui has a switch that can be used at most once: when you arrive at ui and have not yet used its switch, you may activate it on one of its incoming edges vi → ui reverse that edge to ui → vi and immediately traverse it.

The reversal is only valid for that single move, and using a reversed edge costs 2 * wi.

Return the minimum total cost to travel from node 0 to node n - 1. If it is not possible, return -1.

 

Example 1:

Input: n = 4, edges = [[0,1,3],[3,1,1],[2,3,4],[0,2,2]]

Output: 5

Explanation:

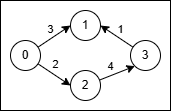
• Use the path 0 → 1 (cost 3).
• At node 1 reverse the original edge 3 → 1 into 1 → 3 and traverse it at cost 2 * 1 = 2.
• Total cost is 3 + 2 = 5.

Example 2:

Input: n = 4, edges = [[0,2,1],[2,1,1],[1,3,1],[2,3,3]]

Output: 3

Explanation:

• No reversal is needed. Take the path 0 → 2 (cost 1), then 2 → 1 (cost 1), then 1 → 3 (cost 1).
• Total cost is 1 + 1 + 1 = 3.

 

Constraints:

• 2 <= n <= 5 * 104
• 1 <= edges.length <= 105
• edges[i] = [ui, vi, wi]
• 0 <= ui, vi <= n - 1
• 1 <= wi <= 1000

 

Solutions

Solution: Dijkstra's Algorithm

• Time complexity: O(n+mlogm)
• Space complexity: O(n+m)

 

JavaScript

/**
 * @param {number} n
 * @param {number[][]} edges
 * @return {number}
 */
const minCost = function (n, edges) {
  const graph = Array.from({ length: n }, () => []);
  const dist = Array.from({ length: n }, () => Number.MAX_SAFE_INTEGER);
  const visited = Array.from({ length: n }, () => false);
  const minHeap = new MinPriorityQueue(({ cost }) => cost);

  for (const [u, v, cost] of edges) {
    graph[u].push({ node: v, cost });
    graph[v].push({ node: u, cost: cost * 2 });
  }

  dist[0] = 0;
  minHeap.enqueue({ node: 0, cost: 0 });

  while (minHeap.size()) {
    const { node, cost } = minHeap.dequeue();

    if (visited[node]) continue;
    if (node === n - 1) return cost;

    visited[node] = true;

    for (const neighbor of graph[node]) {
      const totalCost = cost + neighbor.cost;

      if (totalCost >= dist[neighbor.node]) continue;

      dist[neighbor.node] = totalCost;
      minHeap.enqueue({ node: neighbor.node, cost: totalCost });
    }
  }

  return -1;
};